NTC18 con Straus7 ed EasyOver: cosa cambia nella valutazione della vulnerabilità sismica di strutture in c.a.
Nel presente articolo si considerano le principali modifiche e novità introdotte dalle nuove NTC 2018 e dalla relativa Circolare esplicativa nelle verifiche di vulnerabilità sismica di strutture esistenti in cemento armato.
Dalle NTC08 alle NTC18 con Straus7 ed EasyOver: le novità
Nel presente articolo si considerano le principali modifiche e novità introdotte dalle nuove NTC 2018 e dalla relativa Circolare esplicativa nelle verifiche di vulnerabilità sismica di strutture esistenti in cemento armato.
In particolare vengono esaminate:
- la nuova metodologia introdotta dalle NTC 2018 per la valutazione del punto di prestazione (Performance Point, PP) nella curva di capacità di una struttura determinata tramite analisi statica non lineare;
- le nuove relazioni per la valutazione della resistenza al taglio di travi e pilastri in condizioni sismiche, le quali prevedono una riduzione della stessa in condizioni cicliche, in funzione della domanda di duttilità sull’elemento.
Vengono effettuati gli opportuni richiami normativi, mettendo a confronto le formulazioni proposte dalle NTC 2008, dall’EC8 Parte 3 e dalle NTC 2018; vengono poi eseguiti i relativi confronti numerici, esaminando i risultati delle analisi non lineari statiche e dinamiche. Per la modellazione agli elementi finiti è stato adottato il codice di calcolo Straus7, [9], e il software EasyOver, [10], applicativo di Straus7 per le analisi statiche non lineari di edifici in cemento armato.
I richiami normativi
Il Calcolo del Performance Point
Pur non avendo cambiato l’approccio metodologico rispetto alle NTC 2008, le nuove NTC 2018 e la relativa Circolare esplicativa n. 7 del 21/01/2019 hanno introdotto delle significative novità e modifiche in relazione alla valutazione del Performance Point e della resistenza a taglio di travi e pilastri in condizioni sismiche.
Tali modifiche incidono in maniera non trascurabile sul calcolo dell’indice ζE di vulnerabilità sismica di una struttura esistente.
Per quanto concerne il calcolo della domanda sismica, le NTC 2018 prevedono ora due metodi:
- il metodo A, basato sull’individuazione della domanda anelastica attraverso il principio di uguali spostamenti o uguale energia, analogo al metodo proposto dalla Circolare esplicativa delle NTC 2008, n. 617 del 02/02/2009;
- il metodo B, iterativo, basato sulla costruzione di uno spettro di capacità.
Di seguito si riporta la descrizione del metodo B, ripresa dalla Circolare esplicativa delle NTC 2018:
“Si converte lo spettro di domanda nel relativo spettro sul piano ADRS, in cui le accelerazioni spettrali Se sono rappresentate in funzione degli spostamenti spettrali SDe.
Si effettua una prima stima del punto di prestazione ipotizzando, generalmente, che lo spostamento d*max sia pari a quello di una struttura elastica avente la stessa rigidezza iniziale della struttura analizzata:
d*max(0) = de
Stimato il punto di prestazione (F*max, d*max) sulla curva di capacità del sistema equivalente F*-d*, ad essa si sostituisce una curva bilineare equivalente, in termini energetici, ottenuta adottando un primo tratto con pendenza pari alla rigidezza iniziale della struttura ed identificando la forza F*y e la pendenza del tratto F*y-d*maximponendo l'uguaglianza dell'area sottesa dalle due curve, come mostrato in Fig. 1. 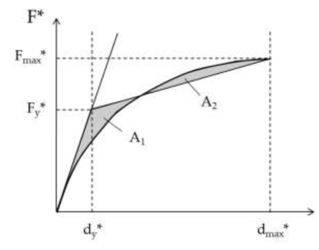
Fig. 1 – Bilinearizzazione equivalente
A partire dalla curva bilinearizzata così definita, si calcola lo smorzamento viscoso equivalente associato, espresso in percentuale, attraverso la seguente relazione: 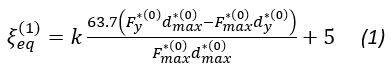
dove il coefficiente k tiene conto delle capacità dissipative della struttura ed in particolare delle caratteristiche del ciclo di isteresi.
Indicativamente, si possono assumere i seguenti valori, a seconda della differente tipologia strutturale:
- strutture ad elevata capacità dissipativa (caratterizzate da cicli di isteresi stabili e ragionevolmente ampi): k = 1;
- strutture a moderata capacità dissipativa (caratterizzate da cicli di isteresi con moderata riduzione dell’area): k = 0,66;
- strutture a bassa capacità dissipativa (caratterizzate da cicli di isteresi con pinching elevato e da una sostanziale riduzione dell’area): k = 0,33;
- strutture dotate di appositi dispositivi di dissipazione: va valutata l’energia dissipata complessivamente, attribuendo alla struttura e al sistema di dissipazione il valore di k corrispondente all’effettiva capacità di dissipazione.
Grazie al coefficiente ξeq così calcolato si abbatte lo spettro di domanda. L'intersezione, sul piano ADRS, fra lo spettro di domanda abbattuto e la curva di capacità del sistema equivalente fornisce il nuovo punto di prestazione, come mostrato in Fig. 2; se esso è caratterizzato da uno spostamento d*max(1) ragionevolmente prossimo a quello stimato in partenza d*max(0), la procedura iterativa ha termine e si ha la soluzione. La procedura è iterativa ed è ripetuta fino a convergenza della soluzione.”
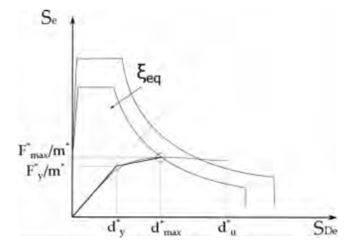
Fig. 2 – Individuazione del Punto di Prestazione
La questione di fondamentale importanza è che in base a questo metodo, a differenza del metodo A, il Performance Point dipende dalle capacità dissipative della struttura. Ciò verrà chiarito anche dal primo esempio illustrato nel successivo Par. 3.1.
[...] CONTINUA LA LETTURA NEL PDF

