Metodo per l’ottimizzazione strutturale topologica di edifici irregolari in muratura armata
Attraverso l’implementazione di un algoritmo per la ricerca dell’eccentricità di impianto (D.M. 17/01/2018) è stato possibile definire un sistema di equazioni non lineari, in grado di ricercare le lunghezze e la corrispondente posizione di ogni singolo pannello murario, sottoposto ad un sistema di vincoli di dimensionamento.
Attraverso l’implementazione di un algoritmo per la ricerca dell’eccentricità di impianto (D.M. 17/01/2018) è stato possibile definire un sistema di equazioni non lineari, in grado di ricercare le lunghezze e la corrispondente posizione di ogni singolo pannello murario, sottoposto ad un sistema di vincoli di dimensionamento. Dopo la descrizione del metodo, l’articolo propone un esempio di ottimizzazione strutturale di un edificio irregolare sottoposto a vincoli dimensionali architettonici. Il contributo si conclude con l’esposizione dei risultati e la descrizione dei possibili sviluppi futuri.
La continua ricerca di forme esteticamente complesse per la realizzazione di nuovi edifici residenziali, commerciali o direzionali tende, sempre più, a separare il flusso progettuale tra parte architettonica e parte strutturale. Dapprima, infatti, si tende a creare la forma architettonica dell’involucro; solo successivamente essa viene sottoposta ad analisi strutturale con l’intento di dimensionare gli elementi portanti (Casagrande, 2018).
Per gli edifici in muratura ordinaria e armata, ad esempio, l’inserimento dei setti di muratura avviene solamente dopo la definizione del ben noto layout architettonico e delle relative esigenze prospettiche ed estetiche.
In un’ottica ideale, invece, il progetto architettonico dovrebbe essere concepito come “fusione” delle esigenze strutturali ed impiantistiche con l’obiettivo di ricercare, pertanto, una soluzione che sia in grado di soddisfare tutte le condizioni al contorno: questo è il caso tipico di ciò che avviene per la realizzazione delle tensostrutture, dove, la forma architettonica è il risultato di un particolare processo strutturale (Mezzi et al., 2006; Casagrande, 2011).
Una metodologia pratica che si sta diffondendo attualmente in altri paesi è quella di progettare con una modalità “semplificata”, attraverso una parametrizzazione di quelle che sono le esigenze statiche e dinamiche che dovrà possedere la nuova costruzione (Meli, 2011; Porst, 2015).
Edifici in muratura e l'irregolarità in pianta
Nel campo della muratura ordinaria e armata, anche la nuova normativa strutturale italiana (D.M. 17/01/2018) al paragrafo 4.5.6.4 ammette la verifica semplificata di edifici in muratura, purché essi rispettino determinati vincoli tra i quali spicca un’altezza massima di interpiano pari a 3,5 m, una snellezza inferiore a 12, una planimetria inscrivibile in un rettangolo il cui rapporto tra lato inferiore e maggiore non sia inferiore a 1/3 e un carico massimo variabile inferiore a 3,00 kN/m2.
Con tali “imposizioni” strutturali, quindi, è possibile concepire un’estetica e una funzionalità attraverso una fusione di tipo strutturale senza incorrere, successivamente, a varianti oppure a problematiche inerenti il comportamento dell’impianto strutturale in condizioni sismiche.
Tuttavia, le imposizioni che rispettano le caratteristiche delle costruzioni semplici si basano sul concetto di regolarità della pianta. Infatti, qualora, l’edificio si scosti da quello che è il requisito geometrico, esso rientra nell’ambito delle strutture definite irregolari e quindi trattato alla stregua delle verifiche per gli edifici ordinari (Petrini et al., 2004).
Attualmente una progettazione attenta alle esigenze sismiche cerca di ridurre al minimo quelle che sono i fattori che amplificano le sollecitazioni sugli elementi verticali, in questo caso, i setti in muratura. Infatti, per gli edifici irregolari, il fattore che amplifica la sollecitazione flettente e il taglio in un ipotetico pannello murario è l’effetto torcente che si genera tra il baricentro delle masse e il baricentro delle rigidezze.
Il processo di ottimizzazione topologica per gli edifici in muratura
Attraverso il concetto base per la progettazione delle tensostrutture (Casagrande, 2011) un nuovo edificio in muratura potrebbe essere concepito a livello strutturale e architettonico seguendo la logica dell’ottimizzazione topologica (Gatti, 2014), già impiegata con successo nel progetto degli edifici in calcestruzzo armato (Kulkarni et al., 2016).
Per quanto concerne il caso degli edifici in muratura ordinaria e armata, il processo di ottimizzazione può essere definito come una sorta di size and topology optimization. Infatti, a livello del singolo pannello murario, l’ottimizzazione riguarda principalmente la dimensione (lunghezza) del setto murario (size optimization), mentre per quanto attiene la distribuzione delle pareti all’interno del layout, l’ottimizzazione si configura come una sorta di ottimizzazione topologica (topology optimization).
Il presente articolo propone un algoritmo per effettuare l’ottimizzazione strutturale topologica di un edificio in muratura armata con una data distribuzione iniziale di setti e una serie di vincoli di forma e spostamento che simulino le esigenze architettoniche. Sfruttando le tecniche classiche di risoluzione dei sistemi non lineare è possibile ricercare un layout dell’edificio tale da rispettare le condizioni iniziali imposte.
Formulazione del procedimento
Come per ogni altro problema similare l’ottimizzazione strutturale la soluzione può essere ricondotta a quello che è l’obiettivo principale. Generalmente l’ottimizzazione strutturale consiste in una funzione obiettivo f dipendente da una serie di variabili x e da una serie di restrizioni che possono essere di disuguaglianza g, di uguaglianza h e di appartenenza ad un dominio D (Baldock, 2007):
• funzione da minimizzare
min f (x) x = (x1,x2, ..., xn)T (1)
• con restrizioni di disuguaglianza
gj(x) d 0 j = 1, ..., m (2)
• con restrizioni di uguaglianza
Hj(x) = 0 j = 1, ..., p (3)
• con restrizioni di appartenenza
xi ∈ Dj Dj = (di, di2, dir); i = 1, ..., nd (4)
Ovviamente le equazioni precedenti rappresentano solo una parte del sistema di ottimizzazione, in quanto, applicazioni complesse possono tenere in debita considerazione, ad esempio, anche le forze di contatto tra vari blocchi (Whiting et al., 2012). Ciò nonostante, per quanto attiene la mera ottimizzazione strutturale dei pannelli murari non ci sono particolari esempi in bibliografia che impiegano un processo di ottimizzazione diretto, se non quelli inerenti le pareti a taglio in calcestruzzo armato (Nikzad e Yoshitomi, 2017).
Per l’ottimizzazione strutturale di un edificio in muratura armata con forma irregolare la funzione da minimizzare potrebbe variare a seconda dell’obiettivo principale. Essenzialmente, per questo tipo di tecnologia costruttiva (muratura armata), la ricerca delle lunghezze minime dei setti non produce un’ottimizzazione strutturale, come potrebbe essere nel caso di telai in calcestruzzo armato, in quanto, l’intera parete risulta comunque un unico sistema globale formato da elementi in laterizio (fasce di piano ecc.)
In base al paragrafo 7.3.5 delle NTC 2018, la risposta strutturale, tralasciando la componente verticale1 del sisma, deve essere valutata applicando la relazione 7.3.10 di seguito riportata:
cx · Ex + cy · Ey (5)
in cui i coefficienti cx e cy assumono, alternativamente, i valori 1,00 e 0,30.
Negli edifici in muratura armata, le componenti sismiche Ei, possono essere generalmente suddivise per le due direzioni fondamentali X e Y, in quanto, per i setti ortogonali alla direzione principale del sisma (effetto fuori piano), si tende ad assumere una rigidezza nulla (Casagrande, 2018).
Ciò che invece può essere dimensionante dal punto di vista strutturale è l’effetto torcente dovuto all’azione sismica. Infatti, il paragrafo 7.2.6 delle NTC 2018 (M.I.T., 2018), prescrive come al centro di massa debba essere attribuita “un’eccentricità accidentale rispetto alla sua posizione quale deriva dal calcolo” in misura non minore del 5% della dimensione dell’edificio in senso perpendicolare alla direzione della forza sismica.
Il momento torcente che si genera dall’applicazione della prescrizione normativa può effettivamente amplificare notevolmente le sollecitazioni nei vari pannelli murari e limitare quelli che sono gli efficaci metodi semplificati per il calcolo, ad esempio, di sistemi confinati (Tena-Colunga e Lopez-Blancas,2011; Meli e Brzev, 2011). Per l’applicazione delle metodologie semplificate si è visto come l’amplificazione del momento torcente sia effettivamente dimensionante qualora il rapporto tra il lato minore e lato maggiore sia, in effetti, inferiore a 1/3 (M.I.T., 2018; Membreno, 2016).
In base a quanto evidenziato, quindi, una riduzione del momento torcente diminuirebbe conseguentemente le sollecitazioni sui pannelli murari. Per definire un processo di ottimizzazione strutturale applicata al sistema costruttivo muratura armata, è quindi necessario costruire quella che è la funzione obiettivo e le relative restrizioni per ricercare una possibile soluzione. In Figura 1 è riporto lo schema base per la definizione dell’eccentricità globale. Dato un certo impianto strutturale generico con i relativi carichi permanenti e accidentali (Figura 1), l’eccentricità che esiste tra il centro delle masse e il centro delle rigidezze genera, in caso di moto sismico, un momento torcente che si può definire di impianto. Secondo i dettami della normativa cogente (M.I.T., 2018), a tale eccentricità si deve sommare l’eccentricità accidentale dovuta alla non permetta definizione del centro delle masse. Questa eccentricità genera un momento torcente accidentale che deve essere opportunamente considerato nella definizione del momento torcente globale.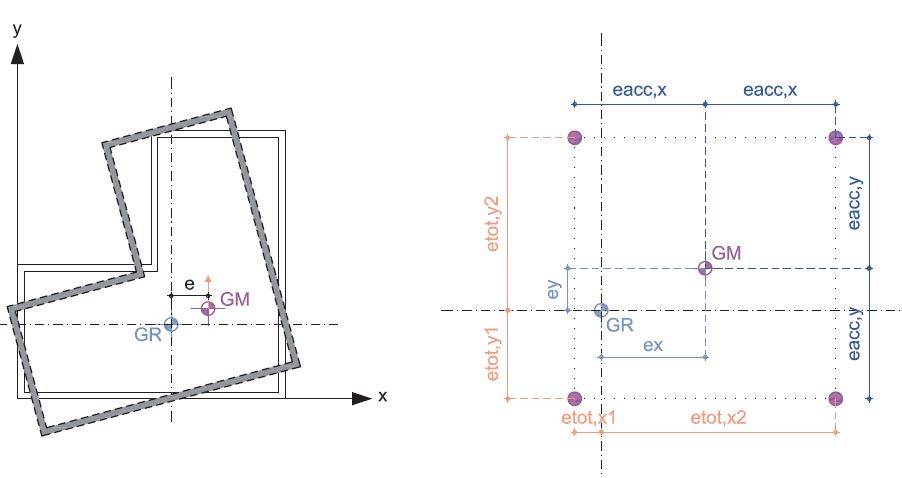
Figura 1 - Definizione delle eccentricità in un impianto strutturale generico.
Per la definizione della funzione obiettivo, quindi, si dovrebbe considerare l’eccentricità accidentale definita con la relazione seguente:
eacc,t = ass(ed) + eacc,d d = (x,y) (6)
ovvero come somma dell’eccentricità di impianto (masse - rigidezze) e dell’eccentricità accidentale da normativa. L’eccentricità di impianto, come anticipato in precedenza, è funzione della posizione del centro delle masse della posizione del centro di rigidezza mentre l’eccentricità accidentale è un valore funzione della geometria dell’edificio, generalmente proporzionale ad una percentuale (5%) della dimensione massima di quest’ultimo. Supponendo, quindi, di fissare una data geometria dell’edificio, avremmo un valore dell’eccentricità accidentale univoco. Essendo il valore dell’eccentricità accidentale derivante dalle caratteristiche puramente geometriche dell’edificio, l’obiettivo può essere ristretto in modo tale da effettuare una mini- mizzazione solamente dell’eccentricità di impianto.
Il processo di ottimizzazione topologica per un edificio di muratura armata può essere applicato in modo agevole, in quanto, questa tecnologia non prevede le restrizioni imposte dai normali edifici in muratura ordinaria. Questo aspetto permette di evitare di inserire nella definizione dei parametri di ottimizzazione una serie di vincoli prescritti dalla normativa: la lunghezza del setto minimo oppure il vincolo di posizione per gli angoli esterni (caso tipico della muratura ordinaria).
>> continua la lettura nel PDF
1 In base al paragrafo 7.2.2 delle NTC 2018 (M.I.T., 2018), la componente verticale deve essere considerata in presenza di elementi pressoché orizzontali con luce superiore a 20 m, elementi precompressi, elementi a mensola di luce superiore a 4 m, strutture di tipo spingente, pilastri in falso. Negli edifici in muratura armata, le condizioni poc’anzi citate sono raramente presenti.
Si ringrazia EUCENTRE per la gentile collaborazione

