Meccanismi di collasso di pareti in c.a.: il modello a fessure spalmate rotanti di Straus7 ed EasyOver
Il modulo “Plate”, del software EasyOver, permette di descrivere il comportamento non lineare di pareti in cemento armato in un’analisi statica non lineare (analisi Pushover).
Tutti gli esempi, riportati nei precedenti articoli [9] e [10] dello scrivente, riguardano analisi statiche non lineari di edifici esistenti modellati con elementi finiti di tipo Beam, eseguite con il codice di calcolo Straus7, [4], e con il software EasyOver, [5], applicativo di Straus7 per le analisi statiche non lineari di edifici in cemento armato.
Nel presente articolo si descriverà il modulo “Plate”, presente nel software EasyOver, [5], il quale implementa un modello a fessure spalmate rotanti in grado di descrivere il comportamento non lineare di pareti in cemento armato in un’analisi statica non lineare (analisi Pushover). EasyOver è in grado di eseguire le analisi non lineari sia di pareti singole che di strutture miste telaio-pareti.
L’utilizzo di tale approccio metodologico può essere vantaggioso, tanto nella descrizione dei meccanismi di collasso di pareti di edifici esistenti in cemento armato, quanto nell’adozione di una progettazione prestazionale di edifici nuovi, in luogo dell’approccio prescrittivo seguito con un’analisi dinamica lineare con fattore di comportamento q.
Vengono dapprima effettuati opportuni richiami teorici per esaminare tutte le modalità di collasso di una parete in cemento armato. Vengono poi illustrati i fondamenti del modello a fessure spalmate rotanti utilizzato per la modellazione del comportamento non lineare di pareti in cemento armato.
Infine, vengono illustrati alcuni esempi applicativi. Per la modellazione agli elementi finiti è stato adottato il codice di calcolo Straus7, [4], e il software EasyOver, [5], applicativo di Straus7 per le analisi statiche non lineari di edifici in cemento armato.
Richiami sui meccanismi di collasso delle pareti in cemento armato
Le NTC 2018, [1], dedicano alle pareti il paragrafo 7.4.4.5, il quale inizia precisando che “si definisce parete un elemento strutturale di supporto per altri elementi che abbia una sezione trasversale rettangolare o ad essa assimilabile, anche per tratti, caratterizzata in ciascun tratto da un rapporto tra dimensione massima lw e dimensione minima bw in pianta lw/bw > 4 (fig. 1).
Le pareti possono avere sezione orizzontale composta da uno (parete semplice) o più (parete composta) segmenti rettangolari. Pareti semplici possono avere appendici con lw/bw w/lw > 2, tozze in caso contrario, essendo hw l’altezza totale della parete (fig. 1) misurata a partire dalla sua base”.
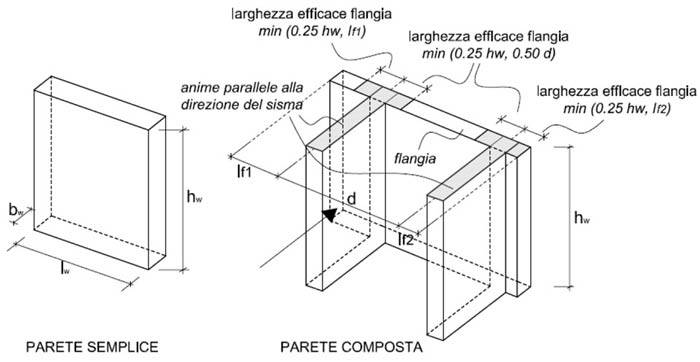
Fig. 1 – Sezioni resistenti delle pareti semplici e composte (la freccia indica la direzione del sisma)
Di seguito si riportano i possibili meccanismi di collasso di pareti in c.a. soggette ad azioni sismiche (si faccia riferimento anche alla fig. 2):
- Pressoflessione
- Taglio
- Scorrimento
- Ribaltamento (sollevamento della fondazione)
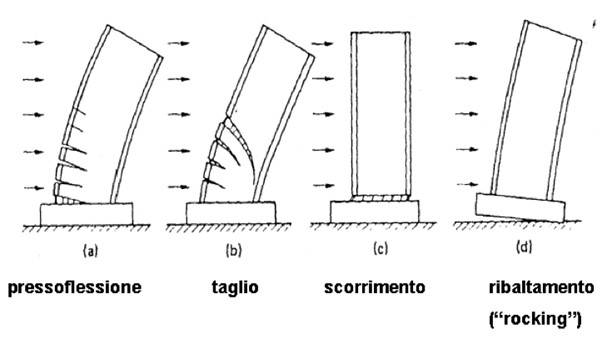
Fig. 2 – Meccanismi di collasso delle pareti in c.a. soggette ad azioni sismiche
Per quanto concerne il comportamento delle pareti in c.a. sottoposte a carichi ciclici, il fattore che maggiormente contribuisce a definire il comportamento ciclico di una parete è il rapporto di snellezza: altezza/lunghezza, hw/lw.
Pareti molto snelle, hw/lw≥2, se correttamente progettate e realizzate, sono caratterizzate da comportamento duttile e da modalità di crisi tipo flessione, simile a quello delle travi.
All’opposto, nelle pareti poco snelle o tozze il fattore maggiormente caratterizzante è il taglio, specialmente la possibilità di crisi per scorrimento da taglio.
Meccanismo di collasso per Pressoflessione
Il principale meccanismo di collasso a pressoflessione per una parete duttile è quello che prevede lo snervamento dell’armatura metallica con la comparsa di ampie fessurazioni da trazione nel calcestruzzo teso e da schiacciamento nel calcestruzzo compresso, ai lembi opposti del nodo parete-fondazione. Lo schiacciamento si verifica solo dopo un certo numero di cicli di carico che ha portato notevoli deformazioni con lo sviluppo adeguato di duttilità. In zona compressa, oltre allo schiacciamento del calcestruzzo, si può presentare l’instabilità delle barre d’armatura longitudinali.

Fig. 3 – Collasso per pressoflessione di una parete di taglio
Collasso per taglio-compressione del calcestruzzo dell’anima
Il collasso per taglio-compressione avviene secondo le modalità evidenziate in fig. 4, nella quale si individua chiaramente, dopo un certo numero di cicli di carico orizzontale, la formazione di fessure diagonali parallele alle isostatiche di compressione. La resistenza a compressione dei puntoni è notevolmente ridotta in caso di sollecitazione ciclica, poiché le lesioni inclinate si formano nelle due direzioni: pertanto, questo porta alla rottura per schiacciamento dei bordi alla base della sezione.
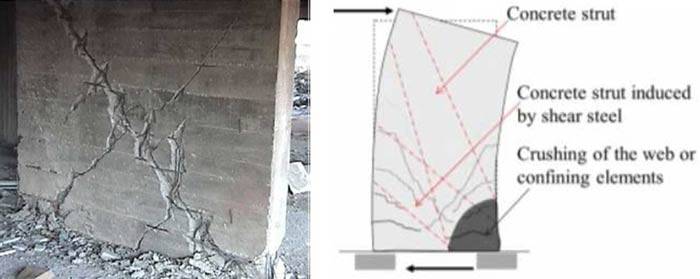
Fig. 4 – Collasso per taglio-compressione di una parete di taglio duttile
Collasso per taglio-trazione dell’armatura dell’anima
Questo tipo di crisi avviene tipicamente nei casi di presenza di un’armatura orizzontale insufficiente (quando l'armatura a taglio è sufficiente, la crisi può avvenire per compressione diagonale, meccanismo esaminato al punto precedente).
Il collasso a taglio-trazione si manifesta secondo le modalità evidenziate in fig. 5, con la formazione di una fessura diagonale più o meno inclinata che attraversa quasi interamente la sezione resistente, creando una pericolosa superficie di discontinuità a resistenza nulla.

Fig. 5 – Collasso per taglio-trazione diagonale di una parete di taglio
Collasso per scorrimento
Una modalità di crisi frequente nelle pareti tozze è per scorrimento, che si verifica quando ad alti livelli di taglio sono associati bassi livelli di compressione assiale.
Questa modalità, simile a quella che si verifica nelle travi soggette ad alti livelli di taglio ciclico, è caratterizzata da eccessivi spostamenti, lungo una lesione orizzontale originata dalla flessione, che causano una drastica riduzione di rigidezza e di capacità dissipativa.
La fig. 6 illustra un esempio di tipico collasso per scorrimento a taglio.
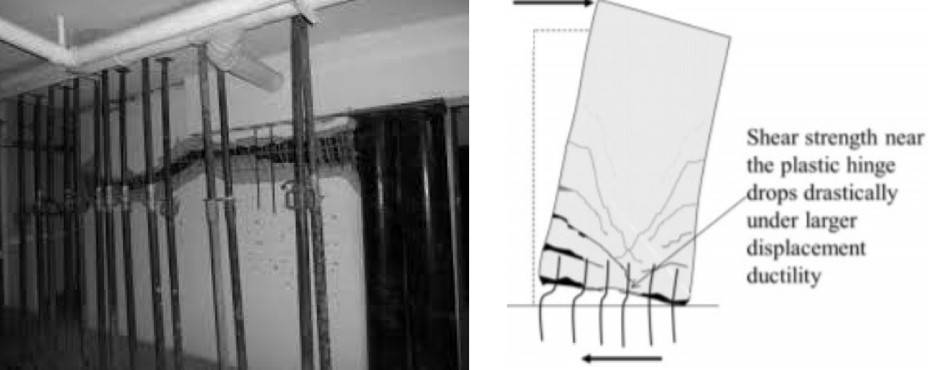
Fig. 6 – Collasso per scorrimento di una parete di taglio tozza
Utilizzo del fattore k, legato al degrado dei cicli di isteresi, in un’analisi statica non lineare
L’analisi statica non lineare consente di eseguire una progettazione con approccio di tipo prestazionale: costruendo la curva Pushover di una struttura (ovvero la curva prestazionale su un piano forza-spostamento o accelerazione-spostamento) è possibile individuare immediatamente il valore del taglio alla base, corrispondente ai diversi stati limite, e soprattutto come, quando e quanto si danneggerà la struttura in esame.
Una critica all’approccio dell’analisi statica non lineare è data dall’incapacità di riprodurre il degrado di resistenza e di rigidezza dovuti ai danni subiti sotto carichi ciclici. La curva di prestazione taglio-spostamento è infatti sostanzialmente un’applicazione di carico monotona sulla struttura.
Questo apparente limite può essere superato grazie al nuovo metodo B, fornito dalle NTC 2018 per il calcolo della domanda sismica in termini di spostamento nella curva in oggetto, discusso più in dettaglio nell’articolo [10] dello scrivente. Tale metodo di calcolo della domanda sismica consente di tener conto delle capacità dissipative della struttura e, in particolare, delle caratteristiche del ciclo di isteresi tramite il coefficiente k, il cui valore varia da 0,33 per strutture a bassa capacità dissipativa (caratterizzate da cicli di isteresi con pinching elevato e da una sostanziale riduzione dell’area) a 1 per strutture ad elevata capacità dissipativa (caratterizzate da cicli di isteresi stabili e ragionevolmente ampi). Chiaramente, a valori più elevati del coefficiente k corrisponderanno maggiori capacità dissipative da parte della struttura oggetto di verifica, ovvero una minore domanda sismica nella curva taglio-spostamento.
Il progettista in questo approccio è quindi chiamato alla scelta del coefficiente k: va detto che il margine di incertezza associato a questa scelta è senza dubbio minore di quello associato alla scelta del fattore di comportamento q (da adottare per abbattere lo spettro di risposta elastico per le azioni sismiche in un’analisi dinamica lineare). Ad esempio, per strutture esistenti progettate prima del 1970 (in particolare prima della legge 2 febbraio 1974, n. 64, recante Provvedimenti per le costruzioni con particolari prescrizioni per le zone sismiche) k assumerà tipicamente valori intorno a 0,33, mentre per strutture esistenti calcolate secondo il DM 16 gennaio 1996 k può assumere valori maggiori, variabili da 0,5 a 0,66. Comunque, essendo il fattore k legato al degrado dei cicli di isteresi, il progettista è chiamato a scelte analoghe, allorquando intenda fare ricorso ad analisi dinamiche non lineari, caratterizzate da un dispendio di risorse computazionali e di tempo notevolmente superiore.
Modello a fessure spalmate rotanti per la modellazione della risposta non lineare delle pareti di taglio in calcestruzzo armato
Il seguente paragrafo intende illustrare un approccio prestazionale, basato sull’implementazione di un modello analitico in grado di analizzare la risposta in campo non lineare delle pareti in cemento armato: trattasi di un modello a fessure spalmate rotanti, applicato agli elementi finiti di tipo Plate, integrato in EasyOver, l’applicativo di Straus7 per le per le analisi statiche non lineari (analisi Pushover) di edifici nuovi ed esistenti.
Il modello analitico alla base del modulo è stato sviluppato a partire dalle teorie “Modified Compression Field Theory” (MCFT) e “Disturbed Stress Field Model” (DSFM), sviluppate dai Proff. Frank J. Vecchio e Michael P. Collins (1986) dell'Università di Toronto, ed è in grado di predire la risposta di elementi in cemento armato, rappresentando il calcestruzzo fessurato come un materiale ortotropo con fessure spalmate rotanti, mentre ciascun layer di armatura viene rappresentato come un materiale ortotropo con rigidezza non nulla esclusivamente nella direzione delle barre dello stesso layer. I vari strati di calcestruzzo e barre di armatura vengono assemblati per formare un materiale elastico anisotropo (fig. 7).
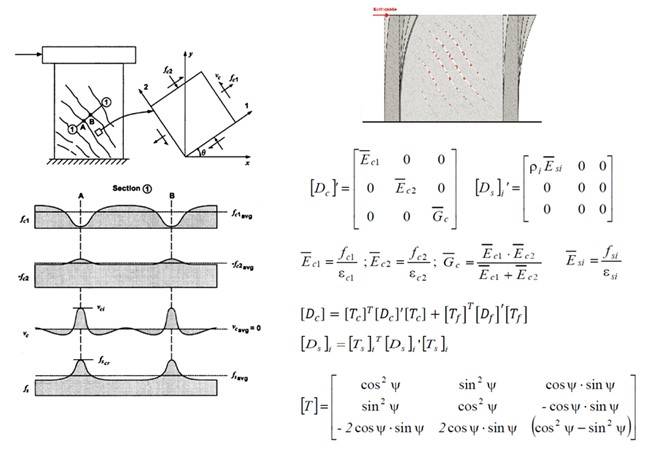
Fig. 7 – Assemblaggio dei layer di calcestruzzo e armatura per formare la matrice di rigidezza dell’elemento
Nel modello a fessure spalmate rotanti, il calcestruzzo fessurato è trattato come un materiale continuo con fessure distribuite sugli elementi Plate. Questa formulazione valuta sia le tensioni e le deformazioni medie (nella regione compresa tra le fessure) che le tensioni e deformazioni locali di calcestruzzo e armatura nelle fessure, oltre alla larghezza e all'orientamento delle fessure stesse durante le varie fasi di carico. Basandosi su tali informazioni è possibile determinare la modalità di collasso di un generico elemento. Le fessure rotanti possono cambiare il loro orientamento, rimanendo sempre collegate ai cambiamenti delle direzioni delle tensioni principali.
[...] continua la lettura nel PDF

Calcestruzzo Armato
Aggiornamenti e approfondimenti sull'evoluzione dei materiali a base cementizia, normative pertinenti, utilizzi innovativi, sviluppi tecnici e opinioni di esperti.

Ingegneria Strutturale
Tutto quello che riguarda il tema dell’ingegneria strutturale: innovazione digitale, modellazione e progettazione, tecniche di costruzione e di...

Progettazione
News e approfondimenti riguardanti il tema della progettazione in architettura e ingegneria: gli strumenti di rilievo, di modellazione, di calcolo...

Sismica
Tutti gli articoli pubblicati da Ingenio nell’ambito della sismologia e dell’ingegneria sismica.

Software Strutturali
Tutto quello che riguarda il tema dei software di calcolo strutturale: modellazione, progettazione, innovazione, normativa, tips & tricks,...
Condividi su: Facebook LinkedIn Twitter WhatsApp

