Investigations of shear resistance related to slab bridges in comparison with international design standards
Investigations of shear resistance related to slab bridges in comparison with international design standards, nonlinear FE-analysis and results of full-scale test series
This research paper deals with different concrete slab bridges, which were built in the years 1930 to 1990 and should be used in their current mode of operation at least until the end of their expected economic lifetime or even further.
The main target of this research was to determine structural reserves of existing slab bridges within the context of the bridge management system nowadays and the differences of the current international standards. To ensure the quality of the results, all investigations are verified by numerical analysis. Finally, the investigations pointed out that 50% of the design resistance of the reinforcing steel in addition to the concrete contribution according to EC 2 show a realistic result for the shear load carrying behaviour of existing slab bridges with bent-up bars.
Furthermore, with the consideration of these calculative assumptions, the normative safety of bridge structures could be achieved and some bridges are still safe to use in their mode of operation, if the maintenance conditions are adequate.
Investigations of shear resistance related to slab bridges in comparison with international design standards, nonlinear FE-analysis and results of full-scale test series
DI Michaela Kopp1, DI Gerald Köck2, FH-Prof. DI Dr. techn. Markus Vill3
1 Department of Civil Engineering, University of Applied Sciences, Vienna, Austria
2 Master student, 2017
3 Department of Civil Engineering, University of Applied Sciences, Vienna, Austria
According to the recalculation of old structures using current standards some bridge structures do not need any strengthening, but many of them need to be strengthened or completely replaced. Due to the conservative approaches in terms of design, it is not possible to provide documented evidence of conformity for slab bridges of the last century. But for all that, these structures are still in use and do not show many noticeable damages.
In addition to that, the Eurocode 2 prescribes that bent-up bars should cover only fifty percent of the entire shear load and should be fully anchored in the compression zone. The executed maintenance inspections do not show relating damages through the service works, consequently the structures are in a good state.
In this way, there is often no option to fulfil the requirements of the current standards for the assessment of the existing bridges, which has to be done, if there is a change due to enlargement of loads. This high level of safety, which happens due to neglected load bearing effects in design, was investigated for existing concrete slab bridges with bent-up bars. The assumptions, was generate referring to the proof of perforation.
Contrary to bent-ups in slab bridges, the provision for bent-up bars in the ceiling refers to the thickness of the slab.
Finally the results of the numerical simulation and the suggestion in this research paper propose fifty percent contribution of the yield strength of bent-up bars as seen in a verification example in Table 1.
Furthermore, the research focused on the differences of the current international standards, therefore 23 existing bridges were analysed given by the example below, figure 1.
To get realistic results all outcomes are compared to the condition of the real structure and with the outcome of the FE-analysis. The FEanalysis represents the modeling of the complete reinforcement. The different standards are compared to their action relating to key attributes like the slenderness, span width, decade, inclination, longitudinal reinforcement, transverse reinforcement, compressive strength and the yield strength of the reinforcement. The majority of these objects have a span, which does not exceed 10m, a slenderness ratio of 15 to 20 and were built in the 1960s and 1970s. Only 8 of 23 bridges were inclined and most of the structures have a characteristic compressive strength of 20 to 30MPa.
To fulfil the load bearing criteria an economical use of reinforcement ratio should guideline the design codes under terms of as much as required but as less as possible.
2 SHEAR LOAD ASSESSMENT OF EXISTING CONCRETE BRIDGES
2.1 Investigations of bridge structures by nonlinear FE-Modeling
For the analysis of the ultimate load, a crosssectional area of the existing reinforcement with the half span was simulated using symmetric conditions.
The half span has a length of 7.2m, the height of the slab varies between 0.66m and 0.8m in the middle of the bridge. The concrete class is C30/37 and the thickness of the concrete cover is about 3 cm.
Furthermore steel plates were used to induce forces into half of the bridge’s structure due to symmetric boundary conditions. The dimensions of the steel plates are about 20cm in length and 3cm in thickness and they positioned at the distance of 3.5 times of the effective section depth. All results are listed in table 1.
The reinforcement of the beam was calculated to the whole slab and the analysis was separated in two load cases. Load case 1, is the support of the beam with the steel plates and load case 2, is the load which induced the prescribed deformation to press the slab downwards.
The load steps with different multiplier are calculated step by step.
The first 40 load steps have a coefficient of 1.0, the next 40 steps work with a coefficient of 0.1 and the next steps are continuously levelled till 120 analysis steps were achieved.
3 NONLINEAR FE-MODELING
3.1 2D-Input Data: Bridge 5
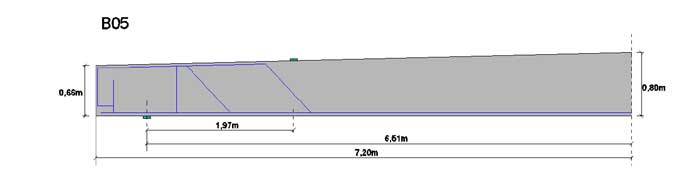
Figure 1. Reinforcement und dimensions of beam B05.
In comparison with other bridge structures, B05 pictures the highest shear resistance, as shown in figure 2 except B09 bridge structure, which was a post-tensioning structure. The stated reasons therefore are the lean beam and the high graduated shear reinforcement ratio of about ρw=0.013. Also, the good concrete quality of C30/37 supports the load-bearing behaviour.
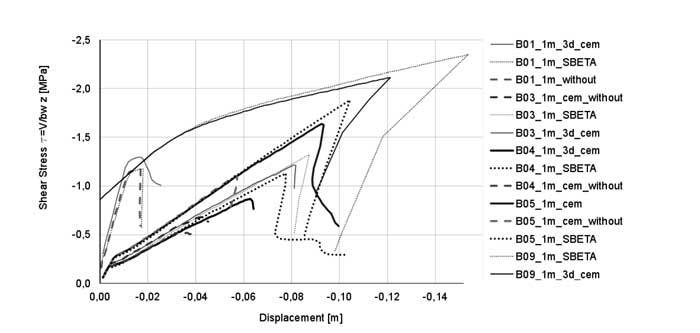
Figure 2. Overview of the parameter study 2D and 3D.
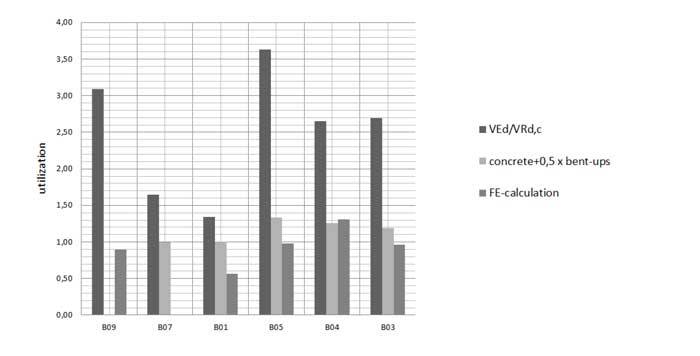
Figure 3. Overview of six different bridges regarding the FEmodeling, EC2 and the research design proposal
4 2D-MODELING
4.1 Bridge 5
The nonlinear-finite-element simulation was carried out with the software ATENA. Therefore, different material models were used to calculate the bridge structures. In total five bridge structures, built between the 1940s and the 1990s, were investigated.
For the simulation, the SBETA Model, as well as a Fracture Plastic Constitutive Model (CC3DNonLin-Cementitious2), was used for analysis of the material model.
4.2 Parameter study 2D beam
Figure 4 shows an ultimate load of 819 kN/m which leads to failure at a displacement of 92 mm. After achieving the maximum load, the iterative calculation process is stopped due to discontinuity.
Figure 4 significantly marks higher shear resistance of SBETA material. This structure consists of a longitudinal reinforcement of Φ30/19.5cm, 2 bent up bar rows with 30mm in diameter and a distance of also 19.5cm in cross section and a concrete strength of C30/37. The ballast is approximately 60cm.
The cross sectional distribution of one track was 4.5m.
Furthermore, the chart describes a shear failure, with big differences due to the shear resistance of structures with and without bent-up bars.
The design shear resistance was achieved by beams without shear reinforcement. According to EC 2 the shear resistance without stirrup reinforcement was about 246kN/m, which points out existing reserves of the load-bearing behaviour in contrast to the FE-model. The FE-Model without bent-up bars faced a resistance of about 560kN/m, this would mean in further consequence, that EC 2 shows a high level of safety compared to VRdc.
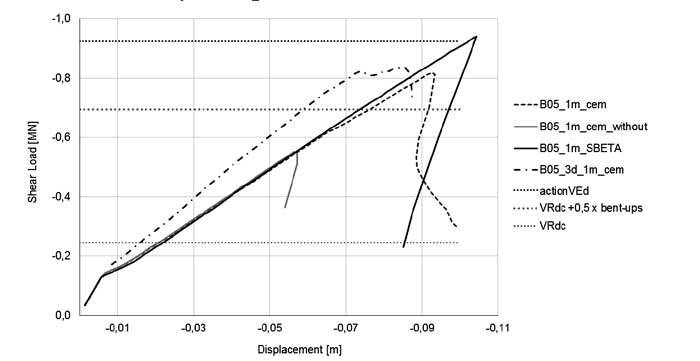
Figure 4. Comparison of differences between shear-load displacement course with and without bent-up bars, the action VEd and also different material parameters.
4.3 Required characteristic action of shear (VEk) under the terms of LM71 and Eurocode 1 for railway bridges
As figure 5 shows, the calculations illustrate an ultimate load level of 819kN/m, whereby the required design load for railways should be considered on a load level of about 925kN/m, as a result of all load combinations and additional load class factors. This implies that the value of the FEmodel overruns the characteristic value of load model 71 according to EC 1, which correlates with other results of this research project.
The current standards allow taking into account 50% of the shear contribution of bent-up bars in addition to shear stirrups. A combination of the contributions of bent-up bars and concrete without shear reinforcement is not allowed in regards with present design standards.
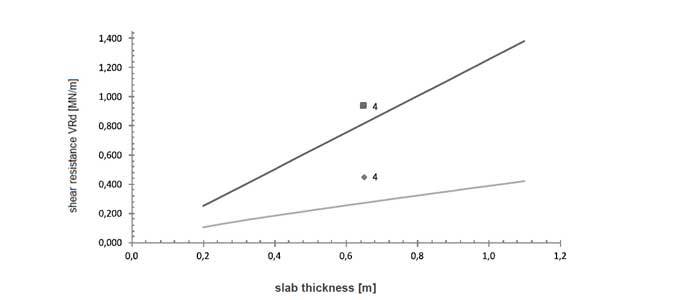
Figure 5. Comparison of shear resistance in regards to the thickness of structure B05 according to EC 2 and EC 1.
4.4 Detailed results of the 2D model
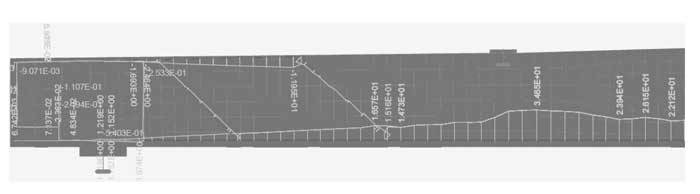
Figure 6. The progress of steel stress σxx of B05 at transition of condition I to condition II [stress; sigma xx; [MPa]].
At the transition of condition I to condition II the maximum stress of the reinforcement is about 15N/mm². This level is reached at load step 5.

Figure 7: Crack pattern and crack openings of structure B05 starting with a width of more than 0.1 mm
The maximum crack width is about 0.8mm, which starts at a nominal stress level of σI=2.75 MPa. The simulation shows the starting of concrete cracking at load step 6, which equals a deflection of 1.0mm.
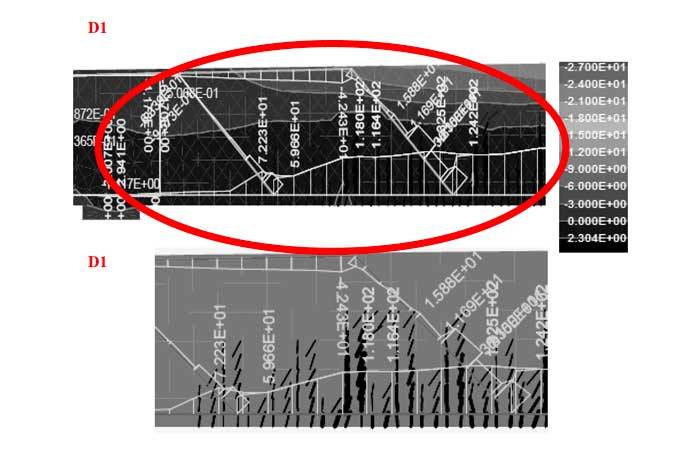
Figure 8. The progress of steel stress σxx at the load concrete resistance level VRdc of EC 2 with a flexural crack width starting from 0.1mm [stress; sigma xx; [MPa]].
The maximal stress of the reinforcement at the level of VRdc appropriate to EC 2 faces a force of 374kN/m, which was achieved at load step 26. This resistance causes a stress of 146 MPa in the reinforcement. At a stress level of VRdc appropriate to EC 2 the reinforcement represents a steel stress of about 60 MPa in the bent-ups, which is set at load step 6. This confirms the assumption that the bent-up bars can only be activated, if there is an increase of strain in the concrete and a crack crosses the shear reinforcement.
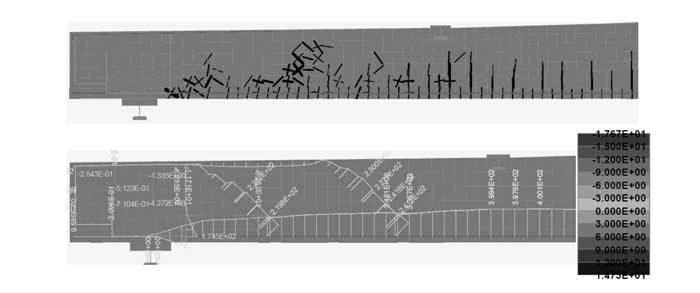
Figure 9 displays the results of the quasi-continuous load, which is about 44% of ultimate load of the FEsimulation.
The chart illustrates the different load levels and points out that there is no exceeding of the ultimate load. The stress in the longitudinal flexure reinforcement has a value of 160 MPa and the stress in the bent-up bars show values of 38 MPa. The results display that the shear forces are mainly covered by the concrete contribution.

Figure 10. The progress of steel stress σxx at ultimate load level [stress; sigma xx; [MPa]].
At ultimate load, which starts at load step 68, the bent-up bars face a shear stress of 250 MPa. Figure 10 shows that the concrete is cracking through the shear reinforcement, which results a rising shear stress. In this connection, the shear reinforcement operates at 50% of its capacity.
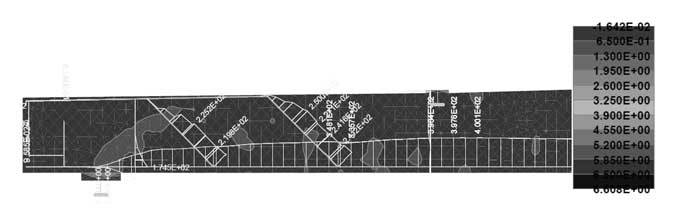
Figure 11. Progress of stressτ xy at ultimate load [MPa].
The area of stress includes shear stress from τ xy -3.0 MPa to +3.0 MPa as peak values.
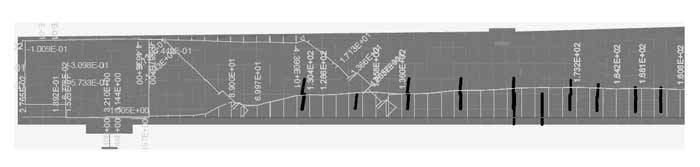
Figure 12. Principal tensile stresses [MPa] and steel stress.
At load step 68, the maximum stress of reinforcement at ultimate limit state represents 250 MPa in the bent-ups. At this condition there are cracks perpendicular to the bent-up bars, as seen in figure 10, so a higher steel stress yields in the bentups.
To sum up the FE-modeling confirm design proposal of 50% bent-up bar utilization due to perpendicular cracks.
5 COMPARISON OF DIFFERENT TEST SERIES
Figure 13 displays the shear stress of the different samples as a function of the inner lever arm. The described bridge structure is noted as B05. The approach exemplifies the 2D and 3D analysis and picture quite similar results. The overview of figure 13 makes clear that the numerical results of this
investigation confirm to the results of other researchers. Further, this work deals with the question of a realistic bent-up bar calculation and how it could be represented in an appropriate
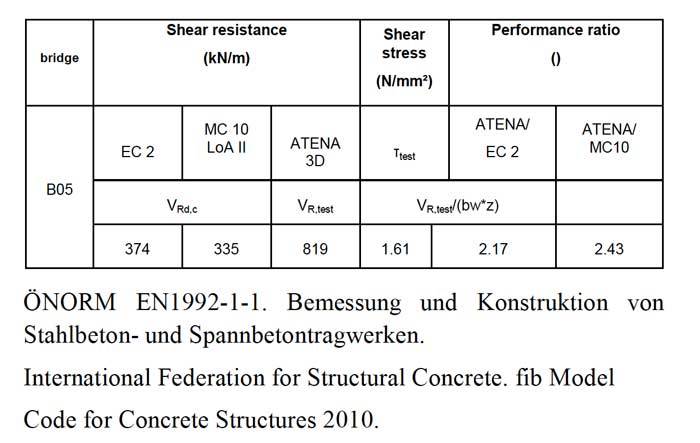
Table 1: Comparison between different design standardizations and the numerical analysis
...
L'ARTICOLO COMPLETO E' DISPONIBILE IN ALLEGATO
KEYWORDS: Railway bridge stock, verification, international design standards, Eurocode 2, shear crack, shear resistance of concrete, stirrups, bent-up bars, longitudinal reinforcement ratio, dynamic factor, slenderness

ICD 2020: L'Evento più importante per gli appassionati di strutture in Calcestruzzo
Nel 2020 si terrà a Napoli la terza edizione degli Italian Concrete Days organizzati da aicap e CTE.
Per saperne di più collegarsi al sito degli ITALIAN CONCRETE DAYS 2020
