Analisi dei meccanismi locali con FaTANext

Il software FaTANext, consente di effettuare l’analisi dei meccanismi locali di strutture in muratura.

È disponibile l’analisi cinematica, sia lineare che non lineare, seguendo le indicazioni delle normative vigenti (D.M. 17/01/2018 e Circolare 7/2019) per SLC, SLV e SLD.

Sono previsti le seguenti tipologie di meccanismo:

• Ribaltamento semplice;
• Flessione verticale;
• Ribaltamento composto;
• Ribaltamento del cantonale;
• Flessione orizzontale.

Modulo Meccanismi Locali
Il modulo Meccanismi Locali può essere utilizzato in maniera indipendente o come Plugin di FaTA Next.

🎯 Offerta Lancio valida fino al 30/06/2025:

Plugin FaTA Next: € 600,00 + IVA
FaTA Next Solo Meccanismi: € 1000,00 + IVA

Scopri tutti i dettagli e ricevi assistenza dedicata accedendo al LINK

  

FaTANext: come si esegue la verifica cinematica dei meccanismi locali nelle strutture in muratura

  

Input dati: come si definiscono i meccanismi e le pareti

I meccanismi da analizzare possono essere definiti sia automaticamente dal software che manualmente dall’utente.

Un meccanismo può essere composto da una singola parete o da più pareti. Se il meccanismo viene definito dall’utente, quest’ultimo ha l’onere di selezionare tutte le pareti che vuole considerare in un singolo meccanismo. Scelte le pareti, il software applica automaticamente tutte le forze che partecipano al meccanismo, differenziandole in stabilizzanti (forze colorate di verde) e destabilizzanti (forze colorate di rosso) e posiziona le cerniere cinematiche, lasciando sempre la possibilità all’utente di modificare queste ultime in funzione delle proprie esigenze (per esempio, per tenere conto di eventuali arretramenti dovuti alla disgregazione della muratura).

Il software FaTANext fornisce anche la possibilità di definire la geometria delle pareti che partecipano al meccanismo. Le singole pareti possono essere opportunamente sezionate per tenere conto dell’effetto di eventuali lesioni, aperture, degradi, ecc. (vedi fig. 1) La geometria delle pareti si definiscono attraverso opportuni strumenti creati appositamente.

  

  

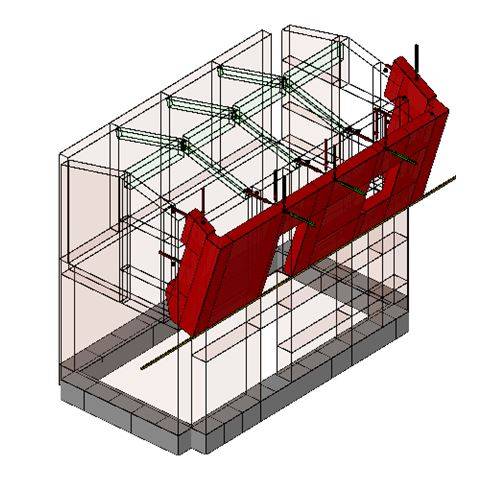
Procedure per definire i meccanismi locali

Il software fornisce l’opportunità di esaminare i vari meccanismi locali seguendo due procedure.

Una può essere quella di definire per intero il modello della struttura, l’altra quella di creare solo la porzione di modello interessata dal meccanismo.

L’adozione di una procedura rispetto all’altra può presentare notevoli vantaggi in funzione dell’obiettivo dello studio. Per esempio, se l’obiettivo è quello di effettuare un intervento locale su una piccola porzione di edificio che comprende solo alcune pareti, è possibile creare un modello strutturale costituito solo dalle suddette pareti e dagli elementi che influenzano direttamente il meccanismo (pareti ortogonali, tiranti, cordoli, ecc.). In questo caso si ha il vantaggio di ridurre l’onere di lavoro necessario per definire il modello strutturale.

I dati necessari ai fini delle verifiche, ricavabili da analisi dinamiche globali (periodo fondamentale, forma modale, ecc.), possono essere gestiti manualmente da appositi comandi.

Se occorre effettuare uno studio più sistematico della struttura, l’edificio può essere modellato per intero, ottenendo i dati ricavabili dall’analisi dinamica, direttamente dal calcolo della struttura effettuato dal software (attraverso analisi dinamica modale).

Il software effettua l’analisi dei meccanismi locali considerando tutte le forze destabilizzanti, come per esempio, inerzie, spinte di archi, tetti, ecc. e stabilizzanti come per esempio, tiranti, cordoli, pesi, sistemi di rinforzo vari, ecc. Inoltre, per rendere lo studio del meccanismo più completo possibile, il software dà la possibilità di gestire forze stabilizzanti e destabilizzanti appositamente modellate dall’utente, da collocare geometricamente in qualsiasi punto del meccanismo.

Tali forze consentono di simulare qualsiasi tipo di dispositivo. Nota la legge (forza-spostamenti – vedi figura 2) che caratterizza la forza, il software la gestisce opportunamente durante il processo di deformazione del sistema.

 

   

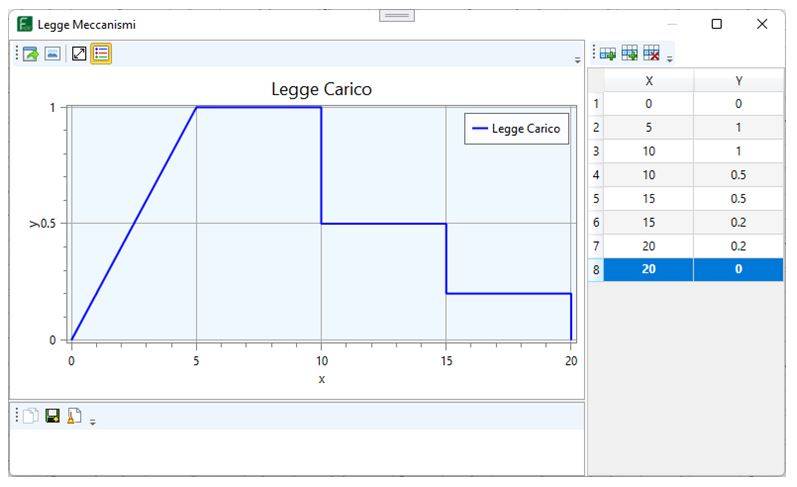
Interpretazione dei risultati: coefficienti di sicurezza e vulnerabilità

Il software FaTANext analizza tutti i meccanismi locali definiti in fase di input, effettuando le verifiche per gli stati limite attivati. L’analisi può essere effettuata con tecniche lineari e non lineari.

Nel caso di analisi cinematica lineare, il software effettua la verifica in termini di accelerazioni, confrontando quella in capacità con quella in domanda secondo quanto prescritto dalle norme. Se il meccanismo è a contatto con la fondazione occorre che sia verificata la seguente condizione:

(1)

Se il meccanismo non è a contatto con la fondazione, occorre tenere conto degli effetti dovuti alle vibrazioni fornite dalla struttura sottostante, per cui, oltre alla precedente relazione occorre verificare anche la seguente:

(2)

dove si indica con a_g l’accelerazione di picco al suolo (fornito dalle coordinate del sito), con S il coefficiente di sottosuolo (fornito da relazione geologica), con q il fattore di comportamento (che per i meccanismi locali si assume pari a 2), con S_ez lo spettro di piano che tiene conto delle vibrazioni della struttura in funzione delle proprietà dinamiche della stessa. Nelle precedenti espressioni, il primo membro rappresenta la capacità in accelerazione della struttura, mentre il secondo membro la domanda in accelerazione. L’accelerazione in capacità si ottiene dalla seguente relazione:

(3)

dove si indica con g l’accelerazione di gravità, con FC il fattore di confidenza (da assumere pari a 1.35 per i meccanismi locali), con e* la frazione di massa partecipante e con a₀ il moltiplicatore dei carichi orizzontali di attivazione del meccanismo.

Quest’ultimo coefficiente si può ricavare dall’equilibrio alla rotazione intorno alla cerniera cinematica di tutte le forze che partecipano al meccanismo o sfruttando la teoria sul principio dei lavori virtuali, secondo cui, il lavoro delle forze esterne deve essere uguale a quello delle forze interne:

(4)

Tutte le forze inerziali, generate dalle forze soggette ad inerzia (come per esempio le forze peso) vengono considerate come frazione di queste ultime. La suddetta frazione è data dal moltiplicatore a₀ che fornisce importanti indicazioni sulle capacità di resistenza sismica di un meccanismo.

Se a₀ >> 0, il meccanismo ha ottime capacità di resistenza alle azioni sismiche.

Se a₀, pur essendo maggiore di zero, assume un valore vicino allo zero, il meccanismo ha limitate capacità di resistenza alle azioni sismiche.

Se a₀ < 0, il meccanismo non è in equilibrio neanche sotto l’effetto dei soli carichi statici. In definitiva, quando si applicano interventi di consolidamento l’obiettivo è quello di far aumentare il valore di a₀.

Nel caso di analisi cinematica non lineare, il software effettua la verifica in termini di spostamento. In quest’ultimo caso, i risultati vengono rappresentati anche graficamente, dove si riportano tutti i passi dello stato di deformazione del meccanismo definiti dalla curva di capacità e tutte le indicazioni necessarie ai fini delle verifiche. È molto intuitiva anche la lettura dei risultati, grazie a una opportuna colorazione degli elementi che caratterizzano graficamente la soluzione del meccanismo. L’analisi cinematica non lineare si articola nei seguenti passi:

• Valutazione della curva di capacità del sistema reale;
• Valutazione della curva di capacità del sistema spettrale;
• Valutazione della capacità di spostamento (d*_SL);
• Valutazione della domanda di spostamento (D_d);
• Confronto tra capacità di spostamento e domanda di spostamento.

L’esito della verifica è da considerarsi positivo quando la capacità di spostamento (d*_SL) è maggiore della domanda di spostamento (D_d):

d*_SL > D_d (5)

La curva di capacità del meccanismo è una curva piana dove in ascissa viene rappresentato lo spostamento del punto di controllo (per quest’ultimo si assume generalmente il punto di massimo spostamento del meccanismo) ed in ordinata il corrispondente moltiplicatore dei carichi orizzontali a. Per definire la curva si considera il sistema in diverse configurazioni deformate, partendo da quella indeformata, e per ognuna delle quali si calcola il moltiplicatore dei carichi orizzontali (analogamente a come fatto per a₀ nell’analisi cinematica lineare nella configurazione indeformata del sistema).

Nota la curva di capacità del sistema reale, è possibile valutare la curva di capacità del sistema spettrale attraverso la trasformazione delle ascisse e delle ordinate:

(trasformazione ascisse da sistema reale a spettrale) (6)

(trasformazione ordinate da sistema reale a spettrale) (7)

Le ordinate vengono trasformate da numero puro ad accelerazioni. Nota la curva di capacità spettrale è possibile ricavare capacità e domanda di spostamento.

La capacità di spostamento (d*_SL) è data dallo spostamento minore ottenuto dalle tre seguenti condizioni:

• il 40% dello spostamento per cui si annulla l’accelerazione spettrale (d₁);
• Lo spostamento corrispondente a situazioni nelle quali si verifichino rotture di elementi, quali catene o altri collegamenti che producono una riduzione della capacità, in termini di accelerazioni, superiore al 50% del valore massimo (d₂);
• Lo spostamento corrispondente a situazioni localmente incompatibili con la stabilità degli elementi della costruzione (ad esempio, sfilamento di travi, collasso di volte, ecc.), nei casi in cui questo sia valutabile (d₃).

d*_SL = min(d₁, d₂, d₃) (8)

La domanda di spostamento si ottiene dalle seguenti espressioni in funzione dello spettro alla base S_De (se il meccanismo è a contatto con la fondazione):

(9)

Se il meccanismo non è a contatto con la fondazione, anche in questo caso, come per l’analisi cinematica lineare, occorre tenere conto degli effetti dovuti alle vibrazioni fornite dalla struttura sottostante, per cui, oltre alla precedente relazione occorre verificare anche la seguente in funzione dello spettro di piano S_ez:

(10)

Per valutare gli spostamenti sopra riportati è necessario valutare il periodo T_SLV da considerare nella valutazione dell’azione sismica dato dalla seguente:

(11)

dove d*_SLV è la capacità di spostamento per lo stato limite di salvaguardia della vita, mentre a*_SLV è la corrispondente accelerazione valutata sulla curva di capacità spettrale (vedi fig. 3).

 

 

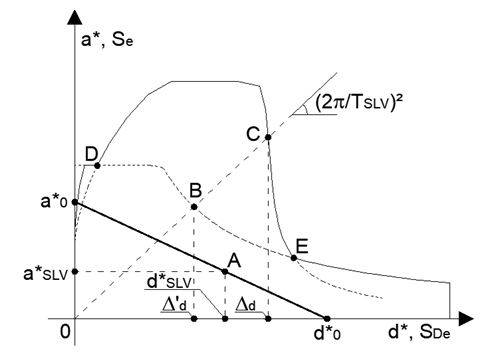
La domanda di spostamento si ottiene solo dall’espressione (9) se il meccanismo è a contatto con la fondazione, mentre se non lo è, si ottiene dal valore maggiore fornito dalla (9) e dalla (10). Graficamente, la domanda di spostamento si ottiene dall’intersezione della retta con coefficiente angolare pari a (2p/T_SLV)² con le curve che definiscono gli spettri (punti B e C in figura 3). Nel caso specifico della figura, la domanda di spostamento si ottiene dall’ascissa del punto C in quanto maggiore di quella del punto B.

Di ogni meccanismo, il software fornisce i risultati, sia in formato testo che in formato grafico. Dalla lettura dei grafici si riesce a valutare immediatamente il comportamento del meccanismo (vedi figura 4).

 

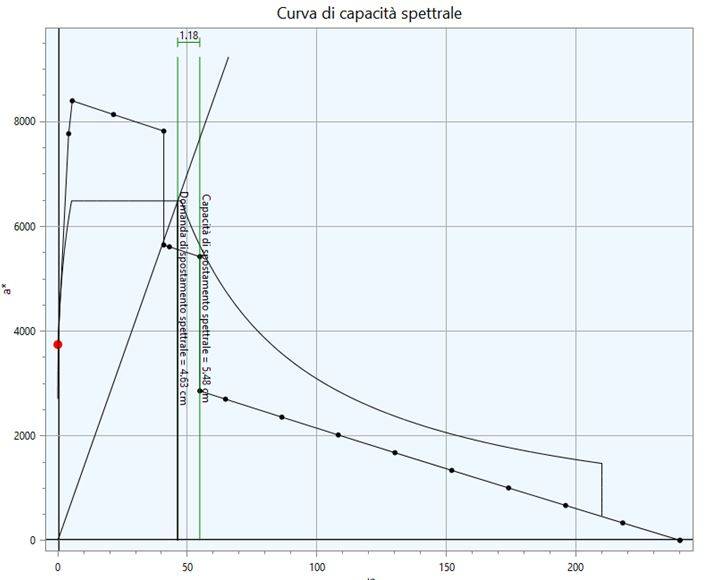
Le linee verticali colorate di verde (che rappresentano la capacità e la domanda di spostamento) indicano che l’esito della verifica è positivo per lo stato limite selezionato (nel caso di esito negativo della verifica le due linee verticali sarebbero state colorate di rosso). Inoltre, il numero collocato tra le due linee rappresenta il coefficiente di sicurezza della verifica (maggiore di zero per esito positivo della verifica, viceversa, minore di zero per esito negativo della verifica). La distanza delle due linee fornisce anche l’entità della verifica.

Se le due linee sono molto distanti e colorate di verde l’esito della verifica è abbondantemente verificato (struttura molto resistente). Se sono molto distanti e colorate di rosso l’esito della verifica è abbondantemente non verificato (struttura molto vulnerabile). Se le due linee sono molto vicine, il sistema è molto vicino al limite di verifica (nella figura che segue si riporta un esempio di rappresentazione dei risultati).

I risultati di tutti i maccanismi analizzati vengono riportati in appositi paragrafi in relazione e viene valutata anche la classe di vulnerabilità sismica della struttura.

 🔍 Vuoi approfondire l’analisi dei meccanismi locali con FaTANext?

Scopri tutte le funzionalità avanzate del software, gli esempi applicativi e le potenzialità per migliorare la sicurezza sismica delle strutture in muratura.

👉 Esplora la pagina di FaTANext

 

Esempi pratici: ribaltamento semplice, flessione verticale e altri casi

Esempio di meccanismo di ribaltamento semplice

Il meccanismo viene schematizzato come unico macro-elemento capace di ruotare rigidamente intorno alla cerniera cinematica e si attiva generalmente per la carenza di connessione tra la parete investita dal sisma e quelle ortogonali (vedi figura 5).

 

 

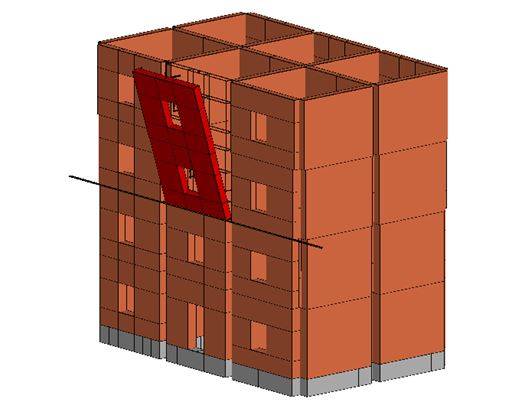
Il comportamento del meccanismo può migliorare attraverso l’utilizzo di dispositivi che ne ostacolano il ribaltamento (tiranti, cordoli, FRP, ecc.) disposti ortogonalmente alla parete che tende a ribaltare. Più i dispositivi sono distanti dalla quota della cerniera cinematica, più sono efficaci ai fini della verifica (aumenta il braccio della forza, che essendo stabilizzante, ne migliora gli effetti).

..continua la lettura dell'articolo integrale nel PDF.

L'articolo continua con:

• Esempio di meccanismo di flessione verticale
  
• Esempio di meccanismo di ribaltamento composto
  
• Esempio di meccanismo di ribaltamento del cantonale
• Esempio di meccanismo di flessione orizzontale

---

PER CONOSCERE COME ANALIZZARE I MECCANISMI LOCALI CON FATANEXT

GUARDA IL VIDEO