Analisi della risposta sismica locale con il FEM
Nell'ambiente Earthquake Engineering di Nòlian All-In-One recentemente (2018) è stato implementato un elemento finito per modellare il suolo con un materiale elasto-plastico a flusso plastico non associativo. Questo elemento si presta ottimamente per ottenere la risposta locale sia in un modello bidimensionale che monodimensionale. Il modello bidimensionale si impone quando si hanno variazioni altimetriche importanti o presenza di differenziazioni laterali rispetto al punto indagato.
Il metodo delle colonne di terreno
Il problema della “risposta sismica locale”, ovvero dell'amplificazione del moto sismico dovuta alla natura del terreno sovrastante lo strato di roccia dove il moto viene definito, è un problema che si sta rivelando molto significativo. Ed è un problema che si può affrontare con gli attuali strumenti di calcolo.
Vi sono dei metodi che schematizzano il terreno con degli smorzatori di Kelvin-Voigt con caratteristiche derivate dalla natura del suolo, si tratta sostanzialmente di una formulazione analitica differenziale risolta con il metodo degli elementi finiti. Questo approccio è molto limitativo perché non consente di descrivere le caratteristiche del terreno in modo preciso e sofisticato e non consente una analisi bidimensionale.
Si tratta cioè di considerare delle colonne di terreno. Questo approccio della colonna è molto più versatile se condotto con elementi finiti sofisticati e non solo banalmente viscosi, con la capacità di considerare più strati e con condizioni sature, non sature e anche di liquefazione. Oltretutto può essere eseguito con qualsiasi programma FEM evoluto senza dover ricorrere a software specializzati.
Earthquake Engineering di Nòlian All-In-One
Nell'ambiente Earthquake Engineering di Nòlian All-In-One recentemente (2018) è stato implementato un elemento finito per modellare il suolo con un materiale elasto-plastico a flusso plastico non associativo.
Questo elemento si presta ottimamente per ottenere la risposta locale sia in un modello bidimensionale che monodimensionale. Il modello bidimensionale si impone quando si hanno variazioni altimetriche importanti o presenza di differenziazioni laterali rispetto al punto indagato.
Il caso studio
In questa nota (integrale in pdf) descriveremo l'approccio monodimensionale tramite colonna di terreno modellata con gli elementi finiti suddetti e valideremo questo modello sia con i risultati ottenuti con il programma OpenSees, con il modello analitico e con il programam Proshake.
Abbiamo impiegato uno degli esempi della documentazione di OpenSees in quanto riteniamo questo caso-prova autorevole e affidabile. Volendo la massima chiarezza nei risultati, impiegheremo un terreno omogeneo ed un accelerogramma costituito da una funzione sinusoidale, questo per non dover valutare la soluzione solo raffrontando graficamente i risultati. Questo non toglie però, come detto, che il modello possa rappresentare situazioni comunque complesse.
Abbiamo voluto quindi ripetere l'esempio di C. McGann e P. Arduino dell'Università di Washington pubblicato tra gli esempi di OpenSees [OpenSees]. I dati dell’esempio sono disponibili sul sito di OpenSees [Opensees].
Come forzante abbiamo impiegato una accelerazione di ampiezza unitaria e frequenza 10 Hz. Questa scelta è dettata dal desiderio di poter confrontare i risultatii con la massima chiarezza,
Il modello richiede alcune accortezze.
Le dimensioni degli elementi devono essere tali da poter cogliere la frequenza più alta fMAX che si desidera considerare. Si definisce il numero di elementi per lunghezza d'onda. La lunghezza d'onda è data da λ = v / fMAX con v la velocità dello strato di suolo. Le condizioni di interfaccia tra roccia e suolo viene realizzata con un dashpot viscoso secondo il metodo di Joiner e Chen [Joiner] che prevede una coefficiente lineare viscoso pari al prodotto della densità del suolo e della sua velocità, che è una impedenza.
I nodi degli elementi devono avere orizzontalmente lo stesso spostamento perché si abbia una azione solo tagliante per cui si usa un constraint che impone spostamenti eguali.
La forzante si otterrà per integrazione dell'accelerogramma al fine di ottenere un velocigramma che, con fattore moltiplicativo pari alla suddetta impedenza, va considerato come una forza agente.
Poiché si assume che vi sia un certo smorzamento, si assegneranno gli opportuni coefficienti di smorzamento di Rayleigh.
Infine su uno dei due nodi superiori si applica un registratore di accelerazione che ci fornirà la risposta a livello del suolo.
Il procedimento è dunque quello di applicare al livello della roccia una eccitazione data dalla normativa e di ottenere un accelerogramma a livello del suolo. Da tale accelerogramma si ottiene uno spettro. Se necessario si può ripetere l'operazione per sette accelerogrammi spettro-compatibili, ottenendo da essi sette spettri che verranno inviluppati. In fine è possibile “lisciare” lo spettro ottenuto secondo il metodo previsto da [GDL, 2008].
Tutte queste funzioni sono automatizzate in Nòlian.
Vediamo ora la validazione dei risultati ottenuti con il FEM. Vediamo innanzitutto l'amplificazione prevista dal metodo analitico che è come segue:
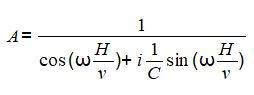
Con i dati del problema abbiamo A = 2.1.
Passiamo all'analisi con Nòlian. Verrà eseguita un'analisi con il materiale in fase elastica e poi una con il materiale in fase elasto-plastica entrambe con il solo peso proprio. L'analisi è un'analisi nel transitorio in quanto la base è libera di muoversi orizzontalmente, vincolata come è solo dal damper, e pertanto darebbe luogo ad una struttura labile, con un'analisi statica. Alle due analisi con il peso proprio seguirà un'analisi con la forzante assegnata. Il passo temporale di questa analisi è opportuno stabilirlo secondo le condizioni di LeVeque [LeVeque, 2007]. Abbiamo applicato un passo di 0.001 s per 1000 passi.
Va detto che nell'ambiente Earthquake Engineering di Nòlian All-In-One, una procedura specifica consente di costruire una colonna di terreno a strati in modo automatico in quanto altrimenti la costruzione di questo modello sarebbe molto laboriosa. [...]
SCARICA IL CASO STUDIO

FEM - Finite Element Method
Gli approfondimenti di Ingenio riguardanti modello FEM (Finite Element Method, Metodo degli Elementi Finiti in italiano).

