L'arco in muratura: un mistero ancora da scoprire
Come dimensionare un arco in muratura? La risposta è contenuta all'interno dell'articolo dove viene fatta un'attenta analisi dei metodi per verificare gli archi in muratura, da quelli storici fino a quelli definiti dalle Norme Tecniche per le Costruzioni 2018
Un libro molto interessante, “The History of the theory of structures” di Karl-Eugen Kurrer, nella parte dedicata agli archi in muratura, apre in questo modo:
“The masonry arch is still one of the mysteries of architecture. Anybody who looks into the history of theory of structures quickly encounters this puzzle, the solution to which has occupied countless numbers of scientists and engineers right up to the present day”“L'arco in muratura è ancora uno dei misteri dell'architettura. Chiunque analizzi la storia della teoria delle strutture incontra rapidamente questo enigma, la cui soluzione ha occupato innumerevoli scienziati e ingegneri fino ai giorni nostri”.
E l’avventura non è ancora finita.
In effetti è molto strano che un tipo di struttura con più di 2000 anni di vita sia ancora oggetto di tante analisi e non si sia ancora giunti a un’unica soluzione condivisa.
Basta una ricerca su Google per scoprire centinaia di documenti, dei quali una buona parte raccontano cosa è stato realizzato nel passato, e poi gli studi recenti, numerosi e con diversi approcci, da parte di quasi tutte le scuole di ingegneria strutturale, italiane e non.
Tanti documenti, ognuno dei quali propone una soluzione, ma in modo un po’ evasivo, nell’incertezza di non aver risolto completamente il mistero.

L'arco in muratura una "struttura smart"
Oggi, usando un inglesismo alla moda, si direbbe che l’arco in muratura è una struttura smart, molto smart.
Perché smart?
La prima ragione: l’arco sfrutta il materiale (naturale o artificiale) nel miglior modo possibile, lavorando principalmente a compressione con tensioni mediamente molto basse, e quindi non soffre lo stress che le strutture moderne sono costrette a sopportare.
Dall’ottocento in poi l’uso di moderni metodi di analisi hanno sempre di più consentito opere leggere e ottimizzate, salvo poi rendersi conto di problemi nel tempo (vedi il degrado del c.a.) e del successivo deterioramento o inadeguatezza per aumenti di carico non previsti.
L’arco, e in generale le strutture in muratura, essendo poco sollecitate, non soffrono aumenti di carico.
La seconda ragione è la grande capacità di sopportare cedimenti e danni localizzati senza gravi conseguenze.
Questa proprietà, vedremo in seguito perché, consente alle strutture ad arco di assorbire, entro certi limiti, fenomeni dovuti a problemi di fondazione, come cedimenti e rotazioni.
La terza ragione è stata la semplicità del dimensionamento di massima. Nel passato si sono usate poche regole per la costruzione, nessun calcolo, nessuna analisi non lineare, semplici rapporti raggio spessore dell’arco e dei piedritti di sostegno.
Regole empiriche, basate sull’esperienza, che oggi siamo in grado di indagare confermandone la validità, dotate di quella semplicità che è alla base di qualsiasi sistema che dura nel tempo.
Insomma: le NTC hanno scoperto l’acqua calda richiedendo il rispetto di criteri di durabilità. Le strutture ad arco hanno da sempre posseduto queste caratteristiche.
Entrando nelle ragioni più analitiche, la gran parte di quanto sopra indicato deriva da una proprietà, apparentemente negativa: la non linearità del materiale.
La muratura non sopporta sforzi di trazione.
Mentre archi realizzati con materiali resistenti a trazione, come il c.a. e l’acciaio, possono portare qualsiasi tipo di carico, per l’arco in muratura i carichi devono essere tali da non provocare distacchi tra i conci.
Per contrastare questo limite interviene la forma.
La curvatura consente di smorzare l’effetto delle spinte orizzontali con i carichi verticali conservando il carico all’interno della sezione stessa, evitandone il ribaltamento.
Se, apparentemente, tutto sembra semplice, quando occorre valutare analiticamente la capacità portante di un arco, sia per carichi verticali che per azioni sismiche, le cose sono molto, molto complesse.
Calcolare la capacità portante di un arco
Contrariamente all’analisi elastica delle strutture, di cui si dispone una trattazione oramai consolidata e condivisa, per il calcolo analitico delle strutture ad arco sono state proposte diverse soluzioni.
La complessità è dovuta, come già detto, prima di tutto alla non linearità del materiale, e alle diverse ipotesi, più o meno semplificative, adottate.
Chi si è occupato di archi in muratura è stato Leonardo.
“L’arco non si romperà se la corda dell’archi di fori non toccherà l’arco di dentro”
Grande studioso delle strutture in muratura e di archi e volte è stato il prof. Heyman, (The Stone Skeleton 1995, The masonry arch.)
Suo il seguente criterio:
“Se esiste una linea delle pressioni per l’arco completo che sia in equilibrio con i carichi applicati, incluso il peso proprio, e che risulti ovunque interna allo spessore dell’arco in ogni punto e in corrispondenza di ogni sezione, allora l’arco può considerarsi in condizioni di sicurezza”.
Sorprendente la somiglianza con il criterio di Leonardo da Vinci, che senza la cultura scientifica moderna, enunciò un principio simile secoli prima.
Ancora più sorprendente la deduzione del prof. Giuffrè, un altro grande studioso della materia:
“Se l’analista riesce a trovare una curva delle pressioni completamente interna allo spessore dell’arco, questo sarà almeno altrettanto bravo a trovarsene una da sé e quindi rimanere in equilibrio”.
Ecco perché l’arco è davvero smart!
I metodi di calcolo per il dimensionamento dell'arco in muratura
I Metodi Storici
I metodi storici per il dimensionamento e quindi anche per la verifica di archi in muratura sono perlopiù di origine empirica, dedotti dall’esperienza, a partire da Leonardo.
A seguire sono state proposte diverse regole, tutte principalmente basate su rapporti geometrici, come la seguente:
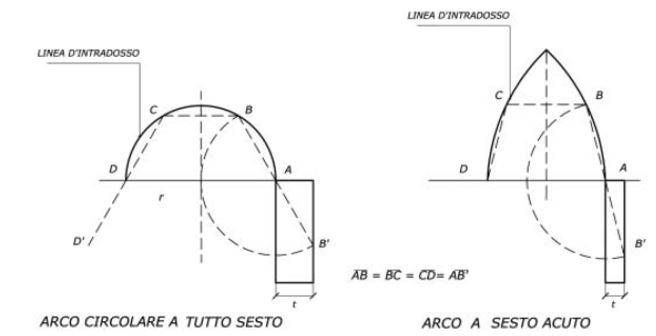
Regola geometrica di Padre Deran, da (Boscotrecase L. 2006), p. 239
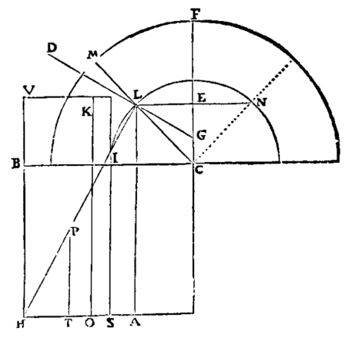
Modalità di calcolo di La Hire per il calcolo dello spessore del piedritto.
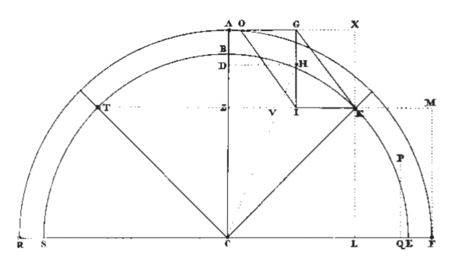
Determinazione mediante procedura grafica dello spessore dell’arco soggetto a carichi permanenti (Couplet, 1730).
I Metodi Moderni
I metodi moderni per la verifica di archi in muratura si possono dividere, approssimativamente, in due approcci, molto diversi tra loro.
Il primo valuta lo stato interno dell’arco, quindi sollecitazioni e tensioni, con una serie di ipotesi più o meno complesse e, attraverso analisi grafiche e analitiche, valuta la resistenza della struttura in relazione ai carichi.
L’analisi di sollecitazioni e tensioni avviene attraverso lo studio della curva delle pressioni.
La prima questione che si presenta, essendo la struttura iperstatica, è che esistono infinite curve possibili, quindi occorre necessariamente semplificare il problema.
In questa semplificazione si nasconde il mistero.
L'approccio Elastico-Lineare
L’arco in muratura è iperstatico, quindi, in linea di principio, è possibile trattarlo con la teoria del corpo elastico; lo si può simulare con un telaio, suddividendolo in tratti lineari o curvi e utilizzare degli elementi “beam”, ma ci sono diverse controindicazioni.
La prima riguarda la definizione delle caratteristiche del materiale, non di facile conoscenza. Ad esempio, per l’arco in mattoni entrano in gioco modulo elastico del laterizio e della malta; i giunti possono avere spessore diverso, il materiale spesso non è omogeneo.
Un’altra questione aperta, derivante dalla logica del solido elastico, è la grande influenza di distorsioni nella struttura per piccoli cedimenti dei piedritti. L’analisi elastica l’insorgere di grandi sforzi interni.
Questo è in forte contrasto con la realtà, dove anche grandi spostamenti non hanno inficiato la stabilità complessiva. Proprio la non linearità del materiale evita questo effetto, e questo è stato chiarito molto bene dal prof. Heyman, con l’idea che le strutture in muratura sono in grado di autostabilizzarsi.
Se anche non si verificassero le due prime questioni, la risposta all’analisi elastica ha senso solo se la curva delle pressioni resta all’interno della sezione dell’arco, meglio ancora se all’interno del terzo medio. Se questo non succede l’analisi semplicemente non ha senso in quanto indurrebbe sforzi di trazione non ammissibili.
L'approccio per elementi discreti e per meccanismi contenuto nelle NTC 2018
Il secondo approccio affronta il problema riducendo l’arco da iperstatico a isostatico, inserendo opportune cerniere sino a rendere l’arco un meccanismo, che può essere studiato con l’analisi limite. In questo caso la verifica della sicurezza avviene attraverso il rapporto tra carico sopportabile e carico imposto.
Questo approccio è quello proposto dalle Norme Tecniche per le Costruzioni per tutte le tipologie di meccanismi locali.
[...] continua la lettura nel PDF
>>> All'interno le indicazioni contenute nelle NTC 2018

