Leggi costitutive avanzate per l'analisi statica non lineare di strutture in muratura

Leggi costitutive non lineari adatte a rappresentare il materiale “muratura”

Nella modellazione strutturale possono essere considerate molte possibili fonti di non linearità: ad esempio, controventi reagenti a sola trazione in telai in acciaio, molle reagenti a sola compressione a rappresentare l'interazione suolo-struttura e leggi costitutive elasto-plastiche assegnate ai materiali.

Le leggi costitutive elasto-plastiche sono utilizzate per rappresentare in modo più accurato la risposta del materiale. In generale, la definizione di parametri aggiuntivi risulta necessaria per rappresentare con precisione la relazione sforzo-deformazione.

In Midas Gen è possibile scegliere tra quattro diverse leggi costitutive adatte a descrivere il materiale muratura:

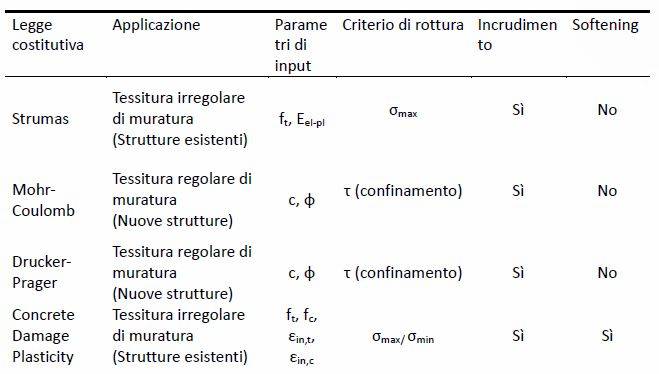
Tabella 1: Leggi costitutive non lineari disponibili in Midas Gen

dove:

• f_t = resistenza a trazione;
• E_el-pl = rigidezza del ramo incrudente (può al limite essere nulla);
• c = coesione;
• f = angolo d’attrito;
• f_c = resistenza a compressione;
• ε_in,t = deformazioni depurate dalla componente elastica a trazione;
• ε_in,c = deformazioni depurate dalla componente elastica a compressione;
• σ_max = sforzo principale di trazione;
• τ (confinamento) = resistenza al taglio dipendente dal confinamento;
• σ_min = sforzo principale di compressione.
  
  

La scelta corretta del modello da utilizzare si basa innanzitutto sulla tipologia di muratura in esame.

Infatti, la rottura può verificarsi con diversi meccanismi, a seconda del processo di realizzazione della muratura stessa. Si possono distinguere due principali modalità fessurative: fessurazione diagonale (governata dalla resistenza a trazione del materiale) e taglio-scorrimento (governato dalla resistenza al taglio). Entrambe le modalità di rottura influenzano le nuove strutture, in cui, a causa della tessitura regolare della muratura, si verificherà una fessurazione diagonale nei giunti di malta tra i mattoni.

Di contro, nelle strutture esistenti possono svilupparsi solo fessurazioni diagonali. Dato che la tessitura della muratura per edifici esistenti di solito non è regolare, la fessurazione diagonale coinvolge sia giunti di malta che mattoni, poiché non esiste un piano preferenziale in cui il danneggiamento possa svilupparsi.

Pertanto, quando si tratta di edifici in muratura esistenti, la rappresentazione migliore si otterrà mediante lo Strumas o il Concrete Damage Plasticity.

Midas GEN per la modellazione e verifica delle strutture

Midas GEN è il software per la modellazione, l’analisi e la verifica di strutture (esistenti e nuove costruzioni) più completo sul mercato nel settore del calcolo strutturale. All’interno del software sono disponibili, inoltre, verificatori per strutture in acciaio e calcestruzzo.

È un prodotto conforme alle NTC 2018 e relativa circolare e dispone anche di verifiche di elementi in CA ed acciaio in accordo alle principali normative internazionali.

Legge costitutiva Strumas

Nella legge costitutiva Strumas devono essere impostati solo pochi parametri, distinguibili tra mattoni, giunti di malta verticali e orizzontali: resistenza a trazione, coefficiente di Poisson, modulo di Young, fattore di riduzione della rigidezza post-picco.

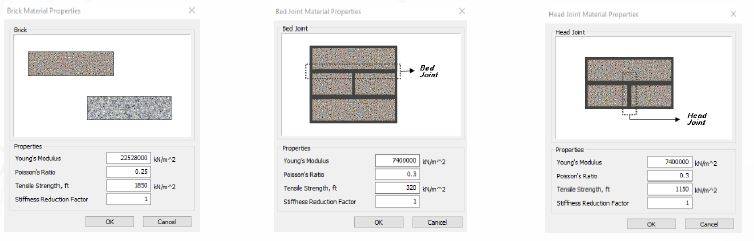
Figura 1: Esempio di parametri per la legge costitutiva Strumas.

Quindi, il software esegue un'omogeneizzazione dei costituenti la muratura (prima in direzione orizzontale e poi verticale) e li converte in un materiale omogeneo, isotropo equivalente. Al termine di ogni step di analisi, i risultati vengono “de-omogeneizzati” in modo da calcolare la quota parte di sforzo relativa ad ogni componente originale. Di conseguenza, è possibile visualizzare, passo dopo passo, i punti di Gauss in cui la tensione principale di trazione supera il limite del materiale (Figura 2).

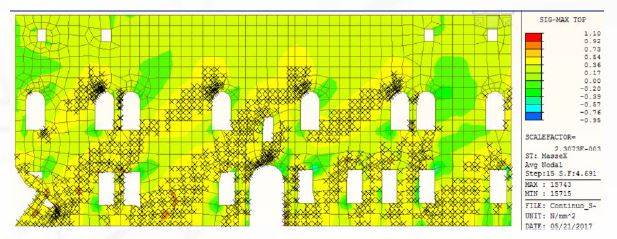
Figura 2:  Esempio di distribuzione diagonale delle fessurazioni ottenuta applicando la legge costitutiva Strumas.

La principale limitazione del modello costitutivo di Strumas è legata al comportamento a compressione dei materiali. Infatti, la resistenza è limitata solo lato tensione, ma non in compressione, per cui il materiale rimarrà indefinitamente elastico.

Concrete Damage Plasticity

Il Concrete Damage Plasticity è una legge costitutiva in grado di rappresentare il comportamento asimmetrico del calcestruzzo o della muratura, discernendo tra risposta a trazione e a compressione. Contempla la presenza di un ramo softening post-picco. Inoltre, con il Concrete Damage Plasticity è possibile considerare il progressivo danneggiamento del materiale sotto carico ciclico. È adatto per materiali quasi fragili come calcestruzzo, muratura e terreni molto addensati.

Parametri

Angolo di dilatanza

Questo parametro ha un chiaro significato fisico, poiché controlla la quantità di deformazione volumetrica plastica che si sviluppa durante la deformazione plastica per taglio. I materiali discreti densi tendono ad espandersi volumetricamente quando sottoposti ad azioni taglianti. Infatti, a causa del loro stato compatto, i grani mutuamente incastrati tra loro non hanno la possibilità di scorrere gli uni rispetto agli altri (Figura 3). 

 

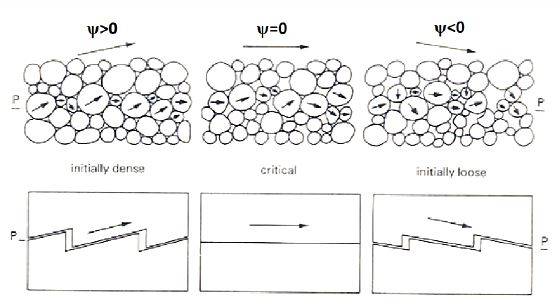
Figura 3: Rappresentazione fisica dell'angolo di dilatanza ψ.

L'angolo di dilatanza può variare tra zero e l'angolo di attrito del materiale. Un angolo di dilatanza pari a zero (ψ=0) significa che il materiale conserva il suo volume quando si verifica una deformazione per taglio.  Al contrario, se ψ=f il materiale si gonfia della stessa quantità con cui scivola, aumentando non realisticamente il suo volume.

Eccentricità

Questo parametro definisce quanto la funzione potenziale di flusso G si avvicina all'asintoto (cfr. Figura 5 e Figura 6). Infatti, il potenziale di flusso G (Figura 4) tende ad una linea retta, quando l'eccentricità tende a zero.

Il potenziale di flusso assicura che il rapporto tra le deformazioni per taglio e quelle volumetriche sia sempre definito in modo univoco.

Il valore del potenziale di flusso predefinito in Midas Gen è 0.1, il che implica che il rapporto tra le deformazioni per taglio e quelle volumetriche si mantiene quasi costante su un ampio intervallo di valori di pressione di confinamento. 

L'aumento del valore dell'eccentricità fornisce una maggiore curvatura al potenziale di flusso, implicando che il rapporto tra le deformazioni per taglio e quelle volumetriche diminuisce più rapidamente man mano che la pressione di confinamento diminuisce. Per valori di confinamento negativi (trazione) le deformazioni per taglio sono quasi completamente assenti e l’intera deformazione plastica si manifesta in modo volumetrico.

[...] CONTINUA LA LETTURA NEL PDF ALLEGATO