Meccanica computazionale e duttilità dei materiali

In questo articolo, l'ing. Roberto Spagnuolo, ci spiega quali sono alcune delle possibilità offerte dalla meccanica computazionale per confrontarsi con il fenomeno della duttilità dei materiali.

Sul ruolo della meccanica computazionale

Citiamo da Wikipedia, leggermente correggendo la traduzione automatica presente sul sito italiano evidentemente eseguita sulla versione del sito in inglese:

La meccanica computazionale è la disciplina che si occupa dell'uso di metodi computazionali per lo studio dei fenomeni governati dai principi della meccanica.

Prima della nascita delle scienze computazionali, viste come una "terza via" oltre le scienze teoriche e sperimentali, la meccanica computazionale è stata ampiamente considerata una sotto-disciplina della meccanica applicata. E' invece ormai considerata una sub-disciplina della scienza computazionale.

Cioè il calcolatore elettronico (computer) non è visto come un esecutore meccanico di formulazioni nate per un uso “manuale” pre-informatica, ma lo strumento per far nascere metodi nuovi impensabili per una esecuzione “manuale”. Gli strumenti teorici offerti da questo nuovo approccio consentono anche di comprendere e analizzare più a fondo certi aspetti del comportamento strutturale. Purtroppo, è un leit-motiv dei miei articoli, soprattutto la regolamentazione invita, o costringe, un uso “primitivo” e limitativo delle possibilità invece offerte da questa disciplina. Il computer è visto come un concorrente da domare e costringere a eseguire compiti con metodi che non gli sono propri. In questo articolo, vediamo alcune possibilità offerte dalla meccanica computazionale per meglio confrontarsi con il fenomeno della duttilità dei materiali.

Duttilità nel progetto antisismico

La duttilità, come è noto, è la capacità di un materiale di subire una deformazione plastica prima di rompersi. Nel caso della progettazione di strutture antisismiche si può impiegare la riserva duttile per dissipare energia deformando la struttura prima del collasso. Questo impiego è troppo noto ai progettisti perché ci si soffermi in questo articolo, piuttosto vogliamo vedere cosa ci offre la meccanica computazionale per “entrare” in questo fenomeno interessante.

E' inutile dire che prima dell'uso del computer si potevano applicare considerazioni generali (come ad esempio fa la nostra normativa classificatoria che classifica appunto bassa, alta duttilità e fragile e duttile). Il computer consente di fronteggiare leggi non lineari che sono caratteristiche della rappresentazione di questo fenomeno. Prima dell'uso del computer ciò era semplicemente impossibile.

Solo per amore della “scienza computazionale” ci piace ricordare il teorema di Green che pone in relazione un integrale di linea attorno ad una curva chiusa semplice e un integrale doppio su di una regione piana limitata dalla medesima curva. Il teorema di Green è del 1828 ma era una splendida conquista teorica, non aveva applicazioni pratiche salvo in uno splendido strumento che qualche non più giovanissimo forse ricorda: il planimetro (Fig. 1). Anche qui un teorema trova applicazione pratica solo tramite uno strumento. Oggi il teorema di Green, tramite il computer, consente di integrare funzioni sul contorno di poligoni del tutto generali con estrema facilità (verrà usata in tutte le analisi sezionali egli esempi che seguono).

Fig 1. Il planimetro

Tornando alla duttilità, nel caso della valutazione del ruolo della duttilità nella progettazione antisismica, il problema si può vedere come un problema di energia. Quello che desideriamo è che l'energia di ingresso dovuta al sisma sia soprattutto convertita in energia di deformazione o isteretica.

Possiamo, grazie alla meccanica computazionale, monitorare l'andamento dell'energia nella struttura.

Precisiamo che le immagini cui faremo riferimento sono tratte da funzioni di Nòlian All-In-One ma che questo articolo non è un tutorial di tale prodotto e che le stesse informazioni si possono trarre da ogni programma che tratti in modo adeguato il problema.

Un esempio

Per fare un ragionamento, prendiamo un oscillatore elementare, modelliamolo con una trave a fibre con le fibre costituite da un materiale elastico-perfettamente plastico che ci permette di dosare la duttilità in modo chiaro. Cioè possiamo modificare facilmente la deformazione di snervamento che come è noto, determina la duttilità del materiale. Lo sottoponiamo ad un'accelerazione impulsiva. Partiamo da una deformazione di snervamento molto alta, poniamo unitaria, per avere un comportamento elastico. Vediamo nel ciclo isteretico (fig. 2) che esso racchiude un'area nulla e cioè l'energia cinetica non viene trasformata in energia isteretica. Possiamo vedere il diagramma che mostra le energie (fig, 3), l'energia di ingresso (sismica) è in rosso, quella di deformazione in verde e quella cinetica in blue. L'energia di deformazione viene completamente restituita ad ogni ciclo e non si ha una isteresi.

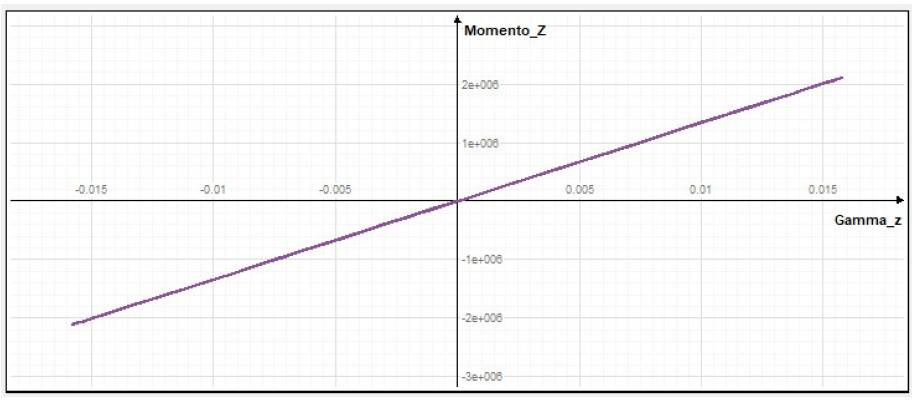
Fig 2. Ciclo isteretico di una sezione di materiale elastico: l’energia l’isteretica è nulla.

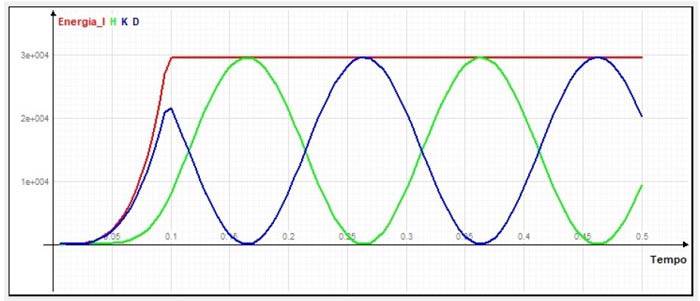
Fig 3. Andamento delle energie di ingresso (rosso), deformazione (verde), cinetica (blu)

Si ricorda che l'isteresi è un fenomeno per cui il valore assunto da una grandezza dipendente da altre è determinato, oltre che dai valori istantanei di queste ultime, anche dai valori che avevano assunto in precedenza.

[...] continua la lettura nel PDF