Analisi di impalcati da ponte autostradali con analogia a grigliato
Nell'articolo verrà discussa la modellazione di impalcati da ponte mediante l'analogia a grigliato. Questo metodo consente di rappresentare gli elementi continui, come le solette e le pareti, di una sezione chiusa con elementi discreti tipo beam. Nei nodi del grigliato si devono riprodurre le deformazioni e le sollecitazioni analoghe a quelle che nascono nella struttura continua. Verranno studiate una serie di sezioni trasversali di impalcato e per ciascuna tipologia sono state valutate le rigidezze degli elementi.
Le rigidezze sono state valutate con la teoria di De Saint-Venant e successivamente corrette in base al comportamento deformativo della sezione. Il comportamento del calcestruzzo e degli elementi del grigliato è basato sulla teoria elastica lineare e con materiale elastico ed isotropo.
L'analogia a grigliato utilizza elementi beam le cui proprietà vanno perfezionate in modo opportuno
L’articolo presenta la modellazione di impalcati da ponte in calcestruzzo strutturale mediante l'analogia a grigliato. Questa tecnica di modellazione utilizza degli elementi beam le cui proprietà non possono seguire le regole della teoria del solido di De Saint-Venant, ma vanno perfezionate in modo opportuno.
Attraverso questa griglia si passa dal continuo al discreto semplificando così l'analisi dell'impalcato la cui risposta è dipendente dalle azioni applicate e dal comportamento del materiale. Questa tecnica, ormai diffusa da molti decenni, rimane ancora un metodo di calcolo molto utilizzato nella pratica progettuale, non solo per la sua semplicità di implementazione, ma anche perché i risultati ottenuti possono essere utilizzati direttamente per le verifiche sezionali.
Questo modo di procedere se pur semplice nella sua descrizione nasconde però delle insidie, legate all'affidabilità dei software che si utilizzano e alla preparazione dell'utilizzatore.
L'utilizzatore deve poter controllare e verificare i risultati ottenuti con sicurezza e anticipare i risultati attesi per le varie azioni e coazioni implementate nel modello; ed in ultimo verificare come l'impalcato dovrà interagire con i vincoli e le sotto strutture. Tutto questo deve passare attraverso la definizione delle rigidezze degli elementi della griglia, come le stesse possono interagire tra di loro in funzione del tipo di impalcato e nel caso dei ponti a cassone includere anche l'effetto della distorsione della cella.
Le softhouse invece predispongono i software e i vari wizard dedicati, in base alle tecniche di calcolo, alle teorie che rappresentano i diversi elementi finiti, agli Standard specifici e agli avanzamenti delle co- noscenze scientifiche, apportate dalle associazioni o dai comitati tecnici internazionali, i quali avanzano le conoscenze nei rispettivi settori. E' chiaro quindi che per eseguire una corretta modellazione è necessario avere software ben sviluppati e utilizzatori con un'ampia formazione tecnica.
Ad evidenziare quanto detto verranno analizzati diverse tipologie di impalcati (solettoni pieni e cavi, solette e travi e sezioni a cassone) descrivendo il loro comportamento tenso-deformativo al fine di definirne le rigidezze. Si mostrerà anche come un grigliato piano non riesce a considerare adeguatamente la deformazione a taglio e la distorsione della sezione. Per risolvere questa limitazione si introdurrà un grigliato 3D e dopo aver discusso il suo funzionamento si passerà a mostrare una sua applicazione per un ponte post-teso, eviden- ziando in esso la modellazione della precompres- sione e della reologia del calcestruzzo. Infine si passerà a discutere l'analisi della sezione dell'im- palcato attraverso metodi di analisi locale, che im- plementano elementi bidimensionali. La figura 1 mostra le sezioni di impalcato considerate nell'articolo.
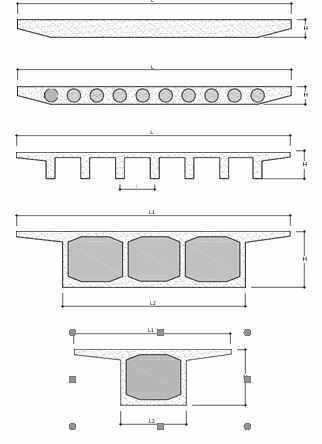
FIGURA 1: Sezioni trasversali di impalcati da ponte in calcestruzzo.
Modelli a grigliato per imaplcati da ponte
L'analisi a grigliato consente di passare dal solido continuo, che rappresenta la reale sezione del- l'impalcato a elementi discreti costituiti da elementi trave (aste) disposte in modo da formare una griglia, anche non regolare, su cui si basa l'analisi in campo lineare. La modellazione però necessita di definire correttamente le rigidezze degli elementi e anche la deformabilità a taglio quando essa è significativa, come per gli impalcati a celle. E' importante sot- tolineare come per uno schema del genere sia cruciale la scelta delle rigidezze dei vari elementi.
Infatti, utilizzando i software dedicati per queste modellazioni le rigidezze sono calcolate in automa- tico, ma occorre comunque poterle verificare o all'occorrenza modificarle, come accade per la rigi- dezza torsionale degli elementi trasversali, quando essa è calcolata in automatico con la teoria della trave alla De Saint-Venant.
Queste proprietà sono importanti per gli elementi del grigliato perché dalla loro interazione, che avviene nei nodi di inter- sezione, si devono riprodurre gli sforzi che la strut- tura continua si scambia nelle due direzioni. Particolarmente importante è anche considerare corret- tamente la distorsione della soletta per effetto membranale dovuta allo shear lag che influisce sulla distribuzione delle tensioni normali nella sezione, mentre per una sezione a cassone la distorsione trasversale riduce la rigidezza torsionale C, rispetto a quella valutata alla Bredt, e aumenta la deformabilità a taglio. La convezione degli assi a cui si riferiranno le rigidezze flessionali I e torsionali C è evidenziata nella figura 2.
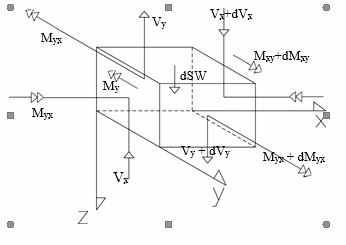
FIGURA 2: Assi sollecitazioni su un elemento di piastra.
Meccanismi che influenzano le rigidezze
Di seguito si discuteranno in modo più approfondito i vari meccanismi che influiscono sulla definizione delle rigidezze degli elementi del grigliato, per poi passare a indicare le varie proprietà meccaniche.
La flessione negli elementi longitudinali è in- fluenzata dalla sollecitazione membranale tangen- ziale, che agisce sulla diffusione delle tensioni nor- mali nella soletta. Tale fenomeno è noto come shear lag ed è comune sia a travi con soletta che a sezioni a cassone. Pertanto, è fondamentale individuare le porzioni delle flange che collaborano con la nervatura attraverso una larghezza efficace (beff). La beff dipende dal punto di flesso del momento flettente, dalle condizioni di vincolo e di come la trave è caricata. Per una trave in semplice appoggio e caricata con un carico uniforme e concentrato in mezzeria la beff vale:
- beff = L/6 per carico uniforme;
- beff = L/8 per carico concentrato.
dove L rappresenta la lunghezza della trave.
... CONTINUA LA LETTURA NEL PDF ALLEGATO
La presente memoria è tratta da Italian Concrete Days - Aprile 2021
organizzati da aicap e CTE
SCARICA L'ARTICOLO COMPLETO IN ALLEGATO
