Comportamento flessionale di tegoli alari precompressi con effetti del secondo ordine

Il comportamento flessionale di tegoli prefabbricati alari con sezione aperta in parete sottile è influenzato da effetti del secondo ordine indotti dall’apertura delle ali. La complicazione del fenomeno porta a ignorarne gli effetti nella pratica progettuale, riservando nei casi più virtuosi a saltuarie elaborazioni complesse agli elementi finiti lo studio di alcune casistiche particolari. La presente memoria illustra un metodo analitico rivolto alla formulazione e alla calibrazione di formule semplici per la stima delle azioni del secondo ordine e un corretto inquadramento progettuale della tematica. La metodologia teorica è applicata a un caso studio di tegolo alare tipo Ondal. Inoltre, analisi numeriche avanzate sono utilizzate per validare la procedura di calcolo proposta.

Alcune esperienze sperimentali hanno indicato che la modalità di rottura per flessione di elementi precompressi con sezione alare utilizzati come tegoli di copertura di edifici prefabbricati sia influenzata dalla deformazione delle ali. In particolare, gli elementi soggetti ad incipiente rottura flessionale mostrano una deformazione trasversale della sezione, accentuata in mezzeria (Dal Lago 1993, 2017; di Prisco et al. 1998, 2002, 2006, 2013; di Prisco & Dozio 2005; Minelli et al. 2006; Belletti et al. 2006, 2016; Lenzi et al. 2009; Diotallevi et al. 2010; Carbonari et al. 2013; Bernardi et al. 2020; Dal Lago et al. 2021).

Tale distorsione sezionale è indotta dalla deformazione flessionale delle ali, e consiste in un fenomeno a sfavore di sicurezza per la resistenza dell’elemento, in quanto è associato ad una riduzione del braccio della coppia interna, indotto dall’avvicinamento dei bulbi compressi e teso. La deformazione flessionale delle ali è indotta dalla combinazione dei carichi gravitazionali che insistono sull’ala stessa, e anche dagli effetti del secondo ordine indotti dalla presenza di una componente di compressione nel bulbo superiore associata alla curvatura della sezione del tegolo.

Pertanto, l’usuale ipotesi di calcolo con sezione indeformabile (rigida) risulta anch’essa essere in generale a sfavore di sicurezza. Ciononostante, tale effetto può essere mitigato proprio limitando la flessione trasversale dell’ala, attraverso la posa di un quantitativo di armatura idoneo.

L’argomento è stato anche affrontato dal punto di vista numerico in modo generico con teorie di ottimizzazione strutturale (Bergamini & Biondini 2004; Balogh & Lógó 2014) e in modo specifico con modelli numerici tridimensionali non lineari sia geometricamente che meccanicamente (Belletti 2009; Bel- letti et al. 2006, 2016, Diotallevi et al. 2010; di Prisco et al. 2013; Carbonari et al. 2013; Bernardi et al. 2020).

Metodologia

Si definiscono effetti del primo ordine tutte quelle sollecitazioni causate dai carichi agenti sulla configurazione indeformata della struttura. Una volta che l'equilibrio della struttura viene perturbato, possono originarsi effetti del secondo ordine tali da incrementare il valore delle sollecitazioni e degli sposta- menti. Gli effetti del secondo ordine possono essere trascurati se il contributo che portano rispetto alla configurazione iniziale indeformata risulta inferiore al 10% (§ 4.1.1.4. delle NTC 2018).

Tuttavia, tale contributo deve essere quantificato per verificare che sia contenuto in tale percentuale, e, come dimostrato più avanti, per tegoli di sezione alare il rispetto di tale requisito è strettamente legato al profilo dell’ala e alla sua armatura. Un approccio semplificato al problema, non affrontato nell’Eurocodice di competenza (EN 1992-1-1:2005), è accennato nella norma di prodotto per elementi alari (EN 13693:2009).

Un metodo per calcolare analiticamente il contributo del secondo ordine è stato proposto in di Prisco et al. (2006, 2013). Tale metodo si basa sull’effetto arco che si viene a creare in virtù della curvatura flessionale del tegolo e della forza di compressione presente nei bulbi superiori. In presenza di curvature, la componente assiale si trova inclinata rispetto all’asse orizzontale, il che crea per equilibrio un carico verticale spingente per effetto del secondo ordine. Tale concetto è illustrato in Figura 1.

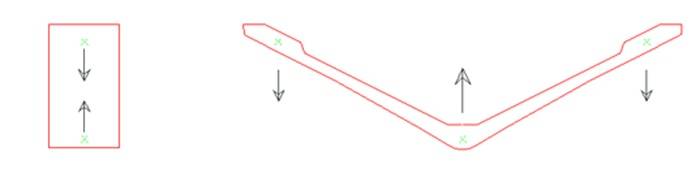
È opportuno rimarcare che tale contributo è presente con segno opposto al lembo inferiore della trave, e che pertanto esso crei uno stato di tensioni autoequilibrate trasversali nell’elemento. Tali azioni del secondo ordine aggiuntive sono tipicamente del tutto ininfluenti per travi di sezione compatta, laddove le risultanti in compressione e in trazione originate dalla flessione della sezione si trovano in asse verticalmente. In tale condizione, possono insorgere esclusivamente deboli tensioni, che non creano normalmente alcun problema al comportamento della sezione.

È opportuno rimarcare che tale contributo è presente con segno opposto al lembo inferiore della tra-ve, e che pertanto esso crei uno stato di tensioni autoequilibrate trasversali nell’elemento. Tali azioni del secondo ordine aggiuntive sono tipicamente del tutto ininfluenti per travi di sezione compatta, laddove le risultanti in compressione e in trazione originate dalla flessione della sezione si trovano in asse verticalmente. In tale condizione, possono insorgere esclusivamente deboli tensioni, che non creano normalmente alcun problema al comportamento della sezione.

Per una sezione alare, invece, la risultante a compressione e quella a trazione risultano essere completamente disassate, inducendo conseguentemente una flessione trasversale della sezione. Tale flessione sollecita le ali. Nell’usuale condizione di verifica con forte carico verticale, inoltre, la forza assiale nel bulbo superiore è di compressione, mentre quella nel bulbo centrale inferiore risulta essere di trazione il che combinato ad una curvatura positiva genera una flessione delle ali che va a sommarsi in segno a quella del primo ordine dovuta ai carichi agenti.

In questo studio, si è scelto di condensare l’azione del secondo ordine in forze discrete concentrate nelle posizioni risultanti. Mentre per il bulbo centrale in trazione tale posizione è facilmente identificabile come il baricentro delle armature di precompressione, per identificare la risultante del singolo bulbo compresso, si rende necessario identificare geometricamente il bulbo superiore, e limitare a tale area il calcolo della risultante.

È opportuno osservare che ignorare le sollecitazioni trasversali del secondo ordine della restante parte della sezione è in generale non a favore di sicurezza, il che è però giustificato dal fatto che tali azioni sono minori (perché minore è la compressione ivi agente in virtù del piccolo spessore della parte centrale delle ali) e che, soprattutto, gli effetti flettenti trasversali già ridotti dall’entità della risultante di compressione sono ulteriormente ridotti dalla vicinanza alla risultante delle trazioni (il baricentro della sezione).

Infine, considerando il carico del secondo ordine puntuale applicato alla sommità dell’ala e non al baricentro del bulbo compresso opera a favore di sicurezza, incrementando il braccio tra le risultanti, a compensazione del contributo ignorato nella parte centrale dell’ala.
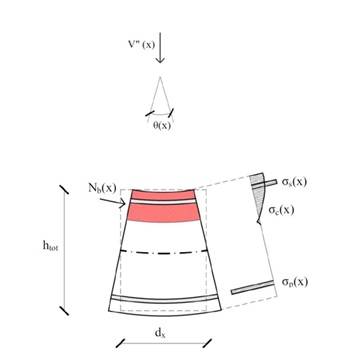
Una volta definita l’area del bulbo superiore, così come in Figura 2, attraverso la larghezza bb e l’altezza hb, si calcola la risultante assiale Nb(x) dalla generica distribuzione di sforzi non lineari illustrate in Figura 3.

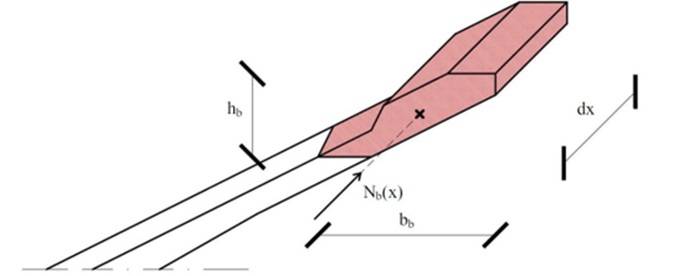
La risultante Nb(x) nei bulbi superiori viene dunque valutata con formulazione integrale sull’area di calcestruzzo e sommatoria dei contributi delle armature lente:

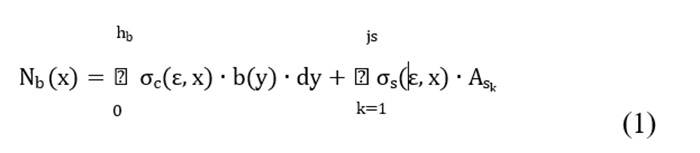
Tale forza (Nb) causa a sua volta un incremento del carico verticale che insiste sull'ala come effetto del secondo ordine:

Si osserva come V" sia proporzionale oltre che a Nb derivante dal momento longitudinale, anche alla curvatura del tegolo, entrambi funzione dei carichi agenti e del diagramma di momento, pertanto non li- neare con l’asse orizzontale del tegolo e massimo in mezzeria.

Sommando V" come se fosse una forza concentrata al carico preesistente sull’estremità dell'ala è possibile determinare il suo effettivo abbassamento dopo aver ricalcolato la distribuzione di momento agente. Sulla base dello schema di sollecitazione citato precedentemente, inclusivo degli effetti del secondo ordine, è quindi possibile valutare lo sposta- mento dell’ala sulla base della doppia integrazione delle curvature lungo il suo sviluppo. La curva di riferimento viene riferita alla sezione debole dell’ala e integrata tenendo conto del suo profilo non costante. Una volta calcolato lo spostamento dala, si conosce la deformazione trasversale della sezione. Considerandone la componente verticale moltiplicando il valore ottenuto per il coseno dell’angolo di inclinazione medio dell’ala rispetto all’asse orizzontale, si può ottenere una geometria modificata della sezione.

In particolare, in via semplificata, si può assumere a favore di sicurezza che la deformazione dell’ala sia lineare con il massimo in punta (dala) e un valore nullo nel centro della sezione. Tale deformata provoca una distorsione della sezione, con avvicinamento delle risultanti a trazione e compressione. Il problema viene quindi risolto implementando la risoluzione sopra descritta per passi con carico incrementale fino a rottura.

CONTINUA A LEGGERE NEL PDF IN ALLEGATO.