Problematiche progettuali relative a controventi in acciaio a diagonale tesa attiva

Nel presente lavoro si vanno ad approfondire una serie di problematiche progettuali relative ai controventi in acciaio a diagonale tesa attiva (detti anche a croce di Sant’Andrea), analizzando sia edifici monopiano industriali che multipiano.

In questa prima parte si analizza il comportamento di questo tipo di controventi proponendo la costruzione di un “fuso” di pushover, caratterizzato da due curve analitiche trilineari di capacità definite su un sistema controventato assoggettato ad una prefissata distribuzione di forze laterali.

La bontà di tale proposta analitica viene evidenziata da una serie di confronti numerici ottenuti con un accurato modello di calcolo, validato sulla base di risultati sperimentali. La proposta viene estesa ad intere strutture monopiano e multipiano, evidenziando per i casi studio analizzati un’ottima corrispondenza con i risultati numerici.

I controventi concentrici a croce di Sant'Andrea per la dissipazione sismica

È noto come l’uso di controventi concentrici a diagonale tesa attiva sia molto ampio in zona sismica per la notevole efficienza di questa tipologia nel resistere alle azioni orizzontali. Durante il sisma l’energia viene infatti dissipata attraverso le diagonali, che plasticizzano in trazione ed instabilizzano a compressione, mentre gli altri elementi come travi e colonne rimangono elastici. Questo tipo di controventi è in particolare ampiamente utilizzato negli edifici in acciaio, sia monopiano (edifici industriali), che multipiano (edifici residenziali, uffici, etc.), per l’elevata capacità dissipativa e la relativa economicità di realizzazione.

In ambito sismico, in generale le normative tecniche nazionali ed internazionali impongono in una analisi elastica un controllo della capacità resistente, dissipativa e duttile della struttura mettendo in conto il contributo delle sole diagonali tese e considerando quelle compresse in bando.

Qualora si voglia mettere in conto anche il contributo delle diagonali compresse, il progettista è obbligato ad effettuare analisi statiche e/o dinamiche non lineari molto accurate, sicuramente più complesse di quelle lineari, ampiamente utilizzate ma molto più realistiche.

Il comportamento isteretico dei controventi concentrici a diagonale tesa attiva è, come noto, fortemente influenzato dall’instabilità degli elementi compressi, dalla plasticizzazione degli elementi tesi, oltre che da fenomeni di pinching quando si ha l’inversione dello spostamento. Per questo motivo il comportamento non lineare è molto complesso da simulare, e può facilmente condurre a stime errate.

Il comportamento isteretico dei controventi concentrici a diagonale tesa attiva è stato analizzato sperimentalmente e teoricamente  da molti autori negli ultimi trent’anni. In particolare, 3 diversi tipi di modellazione sono stati introdotti e utilizzati: modelli fenomenologici, modelli agli elementi finiti al continuo e modelli fisico-teorici. In questi ultimi il controvento viene modellato mediante elementi frame connessi tra loro mediante cerniere.

La plasticità può essere concentrata oppure distribuita lungo l’elemento, secondo una modellazione a fibre. Con questa tipologia di modellazione è possibile ottenere risultati accurati senza avere un eccessivo carico computazionale, cosa che invece avviene per i modelli al continuo, più difficilmente utilizzabili per modellare intere strutture.

Sulla base di studi sperimentali e numerici condotti inizialmente da Black e Wakabayashi è stato ampiamente rilevato come nella realtà un controvento a diagonale tesa attiva abbia un comportamento, sotto un’azione crescente orizzontale monotona o ciclica, caratterizzato essenzialmente da tre fasi (Figura 1): una prima fase nella quale entrambe le diagonali sono attive (fase 1 o di “Pre-Buckling”), una seconda fase dove la diagonale compressa è completamente instabilizzata o sta instabilizzando (fase 2 o di “Post-Buckling”), ed infine, una terza fase nella quale la diagonale tesa entra in campo plastico (fase 3 o “plastica”). 

Risulta quindi ovvio che qualora si voglia effettuare una analisi statica elastica modale utilizzando successivamente lo spettro di risposta o una analisi statica non lineare (pushover analysis), bisognerà tenere in debito conto le tre fasi di comportamento appena descritte.

In questo primo articolo verrà proposto un metodo semplificato per ottenere una curva di pushover trilineare analitica, adatta a rappresentare correttamente le tre fasi di comportamento. Nella seconda parte sarà poi presentato un metodo semplificato atto ad effettuare correttamente un’analisi elastica modale considerando un’opportuno valore di rigidezza delle aste di controvento. 

Leggi la seconda parte dell'articolo sul di controventi a diagonale tesa attiva, dove si presenta un metodo generale di progettazione, applicabile sia ad edifici monopiano industriali che multipiano, dotati di questa tipologia di controvento.

FIGURA 1: Schematizzazione delle tre fasi del comportamento del sistema controventato ad un piano.

FIGURA 2: Schemi per la modellazione dei controventi concentrici secondo le normative, con diagonali tese e compresse a sinistra, e con le sole tese attive a destra.

Curve trilineari proposte

Come visto in premessa, un controvento a croce di Sant’Andrea ha un comportamento caratterizzato da tre fasi (Figura 1):

• nella fase 1 la rigidezza traslante del controvento (K=K₁) è elevata, tutto rimane elastico e non ci sono fenomeni di instabilità;
• nella fase 2 il sistema perde all’incirca metà della sua rigidezza a causa del fenomeno di instabilità della diagonale compressa, trascurando il contributo di quest’ultima si ha (K=K₂=K₁/2);
• nella fase 3 il sistema perde praticamente tutta la propria rigidezza (K=K₃=0) per lo snervamento della diagonale tesa. 

Il comportamento ciclico sarà quindi caratterizzato, a causa delle diverse fasi di comportamento, da importanti fenomeni di pinching nel piano e nel fuori piano del controvento.

Per un controvento mono-piano la rigidezza della seconda fase K₂, nell’ipotesi di trascurare il contributo post critico dell’asta compressa, può essere facilmente calcolata sulla base dello schema di Figura 3.

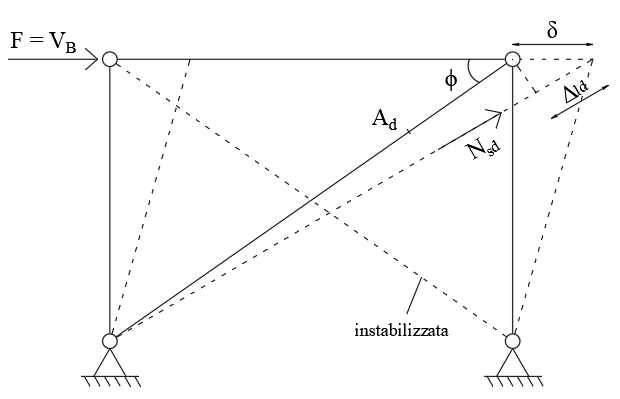
FIGURA 3: Schema per il calcolo della rigidezza della seconda fase di un controvento mono-piano.

L'ARTICOLO CONTINUA...PROSEGUI LA LETTURA SCARICANDO* IL PDF 

 *previa registrazione al sito di INGENIO