Un approfondimento su Taglio e Torsione negli Elementi di Calcestruzzo Armato soggetti ad Incendio
Un approfondimento presentato agli Italian Concrete Days del 2016
La progettazione e la verifica al fuoco degli elementi in c.a. sensibili al taglio ed alla torsione è tuttora un problema aperto, in quanto molto raramente taglio e torsione controllano il comportamento strutturale, e pressochè nulla è l’evidenza sperimentale su collassi controllati dal taglio o dalla torsione in presenza di incendio. Indicazioni utili tuttavia vengono dai modelli di calcolo ben noti per le condizioni ambientali normali e dalla conoscenza dei meccanismi resistenti del calcestruzzo armato.
In questo lavoro - piuttosto generale - i suddetti modelli vengono richiamati per taglio e torsione, ed il loro impiego in condizioni di incendio viene discusso per sezioni compatte ed in parete sottile, rispettivamente con i metodi della sezione efficace e delle zone. Viene anche trattata la sensibilità al fuoco dei vari meccanismi taglio-resistenti. I ruoli delle staffe nel caso di taglio e fuoco e dei puntoni compressi in calcestruzzo nel caso di torsione e fuoco sono critici, semprechè nel caso della torsione si faccia riferimento all’analogia del prisma cavo equivalente.
Taglio e torsione: 1 - INTRODUZIONE
Taglio e torsione in quanto tali intervengono molto raramente nelle strutture in c.a. in quanto nella grande maggioranza dei casi altre – e più rilevanti – sollecitazioni (come la flessione e l’azione assiale) intervengono su porzioni estese della luce, mentre il puro taglio può al più riguardare sezioni singole e la torsione può non essere necessaria per assicurare l’equilibrio allo stato limite ultimo (ACI, 2008).
Il taglio tuttavia si presenta come sollecitazione prevalente in zone localizzate (di discontinuità o Dzones, Reineck, 2002; Reineck e Novak, 2010), mentre la torsione è spesso più un fattore critico per l’intera struttura che per ogni elemento strutturale.
Nel caso della torsione, il trascurare la sua presenza nell’usuale progettazione è giustificato da almeno due altre ragioni: (a) le strutture tradizionali in c.a. sono costituite da telai bidimensionali paralleli collegati da piastre unidirezionali o da sistemi di travi/travetti con soletta collaborante, che trasmettono alle travi di bordo taglio e flessione, ma scarsa o nulla torsione; e (b) l’iperstaticità della maggior parte delle strutture in c.a. fornisce altre modalità resistenti che – grazie ad un aggravio di taglio e flessione negli elementi strutturali – rendono la resistenza a torsione non necessaria per assicurare l’equilibrio (torsione secondaria o di congruenza, in opposizione alla torsione primaria o di equilibrio qualora il comportamento torsionale giochi un ruolo essenziale per assicurare l’equilibrio).
Un’altra e più generale ragione è che nel caso delle sollecitazioni assiali e flessionali la resistenza di un elemento è essenzialmente un problema sezionale (ad esempio, nel caso della flessione la resistenza è controllata da una o più sezioni fessurate in ciascuna delle quali si sviluppa un meccanismo resistente staticamente determinato – una coppia di forze), mentre nel caso delle sollecitazioni di taglio o di torsione la resistenza è controllata da vari meccanismi, che si attivano su porzioni dell’elemento strutturale e che costituiscono sistemi staticamente indeterminati. Tali considerazioni mantengono la propria validità anche in condizioni di incendio, in quanto tutti i meccanismi resistenti attivi in condizioni ambientali normali continuano ad essere attivi anche durante l’esposizione all’alta temperatura.
In tale contesto, si procederà innanzi tutto a richiamare i modelli di calcolo presenti nella normativa del c.a. per la progettazione a taglio e a torsione, in modo da poterli aggiornare all’ambiente fuoco/incendio caratterizzato da alta temperatura e gradienti termici.
Nel caso di taglio, la validità del metodo della sezione efficace o ridotta viene discussa per le sezioni compatte (in cui il campo termico è – di norma – disomogeneo), mentre il metodo delle zone risulta necessario per le sezioni in parete sottile (in cui il campo termico tende ad essere piuttosto uniforme attraverso lo spessore).
Nel caso di torsione, l’analogia del prisma cavo equivalente (o del tubo sottile) fornisce un modello semplice ed efficace, sebbene venga trascurato il nocciolo o nucleo della sezione, il cui contributo alla resistenza torsionale tende ad aumentare con la temperatura, in quanto la parte centrale della sezione in molti casi si mantiene a lungo fredda, cioè all’interno dell’isoterma di riferimento (500°C). (In condizioni ambientali normali la quotaparte del momento torcente assorbita in regime elastico dal nocciolo/nucleo oscilla fra 5-10% e 10-15% a seconda delle dimensioni e della forma della sezione, e della posizione dell’armatura).
Per quanto riguarda infine i vari meccanismi di trasferimento del taglio (staffe, ingranamento delle particelle di aggregato, azione di spinotto ed effetto pettine), l’evoluzione dei loro ruoli con la temperatura è alquanto interessante, seppure complessivamente – a parte le staffe se presenti - si verifichi una generalizzata perdita di efficacia.
2 TAGLIO E TORSIONE NEGLI ELEMENTI DI C.A. ESPOSTI AL FUOCO
Il comportamento degli elementi strutturali in c.a. esposti all’alta temperatura od al fuoco è simile al comportamento in condizioni ambientali normali, in quanto il calcestruzzo continua a rimanere un materiale piuttosto fragile. (Ad alta temperatura la resistenza a trazione diminuisce in proporzione più di quella a compressione). Il calcestruzzo quindi cede in trazione fessurandosi, ed inizialmente la fessurazione è controllata dalle tensioni principali.
Per quanto riguarda invece l’armatura (supposta metallica) il suo comportamento tende a virare con la temperatura, da elasto-plasto-incrudente ad elastoplastico o addirittura a rigido-plastico a temperature molto elevate (oltre 500°C), potendosi trascurare il ramo elastico rispetto all’esteso ramo plastico.
Le fessure tendono inizialmente a formarsi a 45° rispetto all’asse dell’elemento strutturale, se taglio o torsione controllano il regime statico. Nel caso del taglio tuttavia, le fessure tendono a divenire verticali verso l’intradosso (la cui superficie è scarica) in zona tesa, mentre tendono ad appiattirsi in prossimità dell’asse neutro, tanto più quanto più si avvicinano alle fibre compresse.
Nel caso del taglio, la formazione di fessure inclinate sull’asse di circa 40-45°, tipiche degli elementi in c.a. dotati di armatura trasversale a taglio, suggeriscono un comportamento a traliccio bidimensionale (traliccio di Mörsch-Ritter, Figura 1a, sinistra), mentre la formazione di fessure piuttosto appiattite sull’asse, tipiche degli elementi in c.a. privi di armatura trasversale, suggeriscono un comportamento ad arco-tirante (Figura 1a, destra).
Nel caso di torsione, solo gli elementi rinforzati longitudinalmente e trasversalmente sono efficaci; le fessure tendono a svilupparsi secondo spirali inclinate di circa 45° (se è assente l’azione assiale di compressione), poste nello strato più superficiale, con la formazione di un traliccio spaziale (Figura 1b).
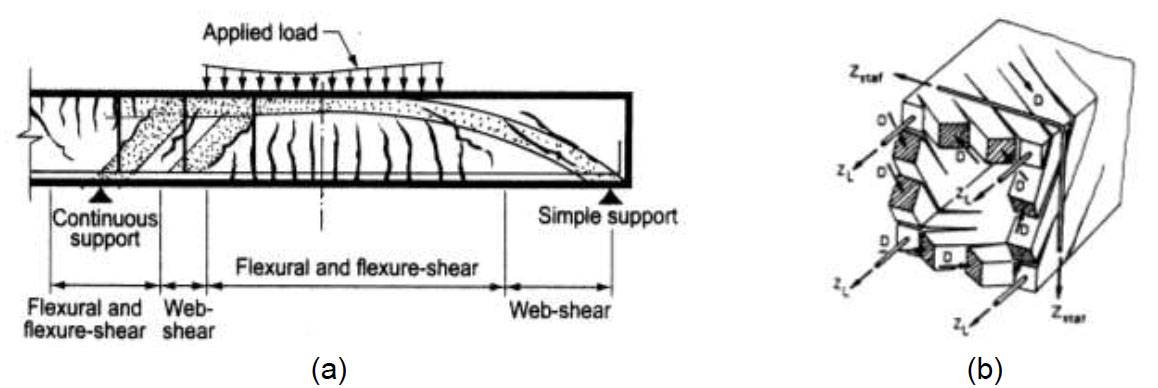
Figure 1. R/C beam (a) in shear, working as a truss system consisting of struts and ties (left) or as an arch-and-tie system (right), in members provided with/devoid of transverse reinforcement, respectively; and (b) in torsion, working as a 3D truss system. Figura 1. Trave in c.a. soggetta a taglio (a) con formazione di un traliccio a puntoni e tiranti (a sinistra) ovvero di un sistema ad arco e catena (a destra), rispettivamente in elementi con/senza armatura trasversale; e soggetta a torsione (b), con formazione di un traliccio tridimensionale. Fig.1a: adapted from/adattata da ACI 318M-08.
Fig.1b: from/da Fuchssteiner, see/si veda Leonhardt in “Spannbeton für die Praxis”, Ernst Verlag, Berlin (1973).
3 MODELLI DI CALCOLO A TAGLIO ED A TORSIONE
Gli stessi modelli impiegati per taglio e torsione nell’ordinaria progettazione a temperatura ambiente possono in via di principio essere impiegati anche nella progettazione al fuoco, purchè le proprietà meccaniche dei materiali e/o le caratteristiche geometriche delle sezioni vengano aggiornate sulla base dell’alta temperatura raggiunta durante l’incendio.
Va tuttavia detto che i modelli introdotti a temperatura ambiente non sono stati mai validati in condizioni di incendio, come chiaramente riconosce l’Annesso D di EC2 (2004), che recita: “…i collassi dovuti a taglio e a torsione sono molto rari …. I metodi di calcolo … non sono completamente verificati (per le condizioni di incendio) ..” e ciò nonostante il numero non piccolo di lavori dedicati al comportamento strutturale al fuoco (si vedano – ad esempio – Kordina, 1979; Hertz, 1985; Ellingwood & Lin, 1991; Felicetti & Gambarova, 1999; Kodur & Hatinger, 2011; Smith et al., 2011).
Nel caso del taglio, può essere usato il metodo molto semplice della sezione ridotta o sezione efficace, che si basa sulle seguenti ipotesi:
- nessun danneggiamento nel calcestruzzo e nell’armatura che - ad una assegnata durata di incendio - siano all’interno o sul contorno dell’isoterma di riferimento (500° per il calcestruzzo ordinario); le resistenze sono quindi le stesse che a temperatura ambiente;
- totale danneggiamento nel calcestruzzo posto all’esterno dell’isoterma di riferimento (nessuna resistenza residua);
- in ciascuna delle barre d’armatura esterne all’isoterma di riferimento, la resistenza è quella corrispondente alla propria temperatura, così come risulta dall’analisi termica della sezione.
Questo metodo è stato inizialmente introdotto per la flessione in presenza di incendio standard, ma è stato poi verificato – ed accettato – anche per la presso/tensoflessione. Le sue ipotesi peraltro non sono in contrasto con il comportamento a taglio.
Un metodo concettualmente simile, ma più preciso è quello delle zone, che si basa sulla suddivisione in strisce della sezione (in genere parallelamente alle isoterme e quindi alle superfici riscaldate più estese), permettendo di valutare uno spessore efficace (mai maggiore di quello geometrico); ogni zona è
a temperatura uniforme (pari alla sua temperatura media), sia per il calcestruzzo che per l’armatura.
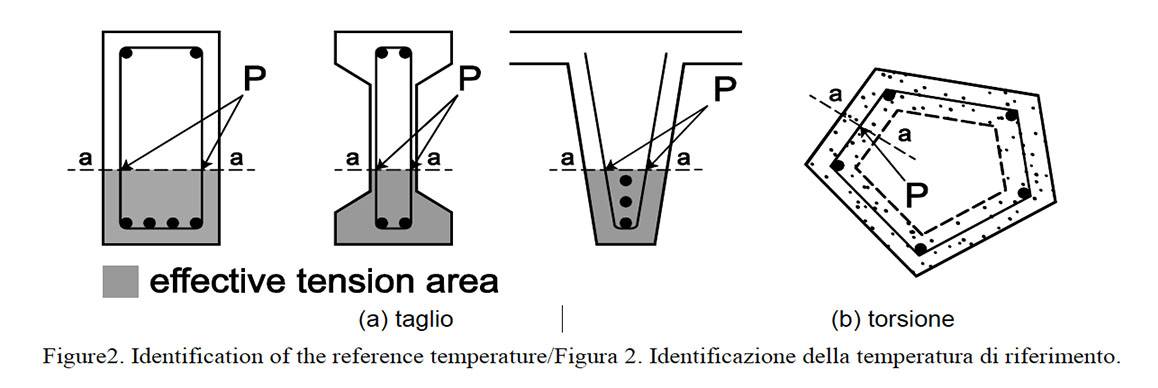
Nelle verifiche al fuoco di sezioni soggette a taglio, tutti e due i metodi possono essere usati, purchè la temperatura nelle staffe sia valutata nel punto di massima sollecitazione (punto di riferimento P, Fig. 2a. Questo è un aspetto chiave in quanto la temperatura nelle staffe non è uniforme, tendendo a decrescere verso la parte alta della sezione, di modo che la temperatura media nelle staffe è inferiore a quella del circostante calcestruzzo (Tattoni, 2005; Campanale, 2005). In EN 1992-1-2 si suggerisce di fare riferimento al punto P posto sulla corda a-a (Fig. 2a) fra l’area efficace a trazione ed il resto della sezione (EC2, 2005). Sempre secondo EN 1992-1-2 la posizione di P dipende dalla posizione delle staffe e delle fessure immaginate a 45°. La temperatura delle staffe è comunque poco variabile, essendo le staffe parallele alla superficie esposta al fuoco.
Per quanto riguarda le barre longitudinali, le proprietà meccaniche dipendono dalla loro temperatura, che coincide con quella del calcestruzzo adiacente, così come fornita dall’analisi termica.
Nel caso della torsione, il concetto di sezione ridotta od efficace confluisce nel concetto di prisma cavo equivalente, ove le caratteristiche meccaniche dei due materiali – calcestruzzo ed armatura - vanno aggiornate in base alle rispettive temperature medie.
Barre longitudinali, staffe e puntoni di calcestruzzo contribuiscono alla resistenza a taglio. Il punto di riferimento P (Figura 2b) può essere scelto a metà dei lati del prisma (corda a-a).
Per la valutazione della capacità portante a taglio e a torsione, sono riportate le equazioni fornite da EC2 (2005) per γc = γs = 1;
l’isoterma di riferimento (se richiesta) è quella di 500°; non sono riportate tutte le limitazioni nell’uso delle equazioni.
Prosegue in allegato
A Napoli dal 14 al 17 aprile 2021 la terza edizione degli Italian Concrete Days di aicap e CTE.
IL PIU' IMPORTANTE EVENTO TECNICO/SCIENTIFICO SUL CALCESTRUZZO IN ITALIA
Ecco le informazioni per partecipare agli Italian Concrete Days 2020 di aicap e CTE a Napoli

Calcestruzzo Armato
Esplora la guida completa sul calcestruzzo e sul calcestruzzo armato, due elementi fondamentali nell'edilizia. Scopri le composizioni, come l'integrazione di fibre metalliche e polimeriche, e le ultime innovazioni che migliorano le proprietà strutturali. Aggiorna le tue conoscenze sui materiali cementizi per una comprensione avanzata e applicazioni ottimali.


