La bellezza misteriosa di e di Eulero, la base dei logaritmi naturali

Su Ingenio non è la prima volta che parliamo di numeri e matematica. Lo abbiamo fatto con i numeri perfetti,  di numeri arabi, greci, romani e indiani, di quadrati magici e, ora, riprendiamo un numero misterioso e fantastico, il numero di Eulero, il numero e, noto anche come base dei logaritmi naturali.

Il numero e è irrazionale, il che significa che non può essere espresso come una frazione di due interi, e il suo valore approssimato è circa 2,71828.

Ma la vera curiosità emerge quando consideriamo la formula di Eulero, una delle equazioni più belle e sorprendenti in matematica:

e^iπ+1=0

Questa formula, chiamata l'identità di Eulero, collega cinque delle costanti matematiche più importanti:

• il numero e,
• il numero π
• l'unità immaginaria i (che è la radice quadrata di -1),
• il numero 1,
• e lo 0.

La bellezza di questa identità sta nella sua semplicità e nella profonda connessione che stabilisce tra concetti matematici fondamentali, unendo l'analisi matematica, la trigonometria e l'algebra in un'unica, elegante formula.

Chi era Eulero

Leonhard Euler (1707-1783) fu uno dei matematici più prolifici e influenti della storia. Nato a Basilea, in Svizzera, Euler trascorse gran parte della sua vita professionale a San Pietroburgo, in Russia, e a Berlino, in Prussia.

Contribuì a numerosi campi della matematica, tra cui la geometria, la trigonometria, l'algebra, la teoria dei numeri e l'analisi matematica. Euler è noto anche per i suoi lavori in meccanica, fluidodinamica, ottica e astronomia.

Euler era eccezionalmente produttivo, avendo scritto più di 500 libri e articoli nel corso della sua vita. La sua capacità di lavorare in diversi campi della matematica e di introdurre nuovi metodi e concetti lo ha reso fondamentale per lo sviluppo della matematica moderna.

Molte delle notazioni matematiche oggi in uso sono state introdotte da lui, tra cui la notazione per la funzione esponenziale e, il simbolo i per l'unità immaginaria, e fu tra i matematici a sviluppare l’uso della lettera π per indicare il rapporto tra la circonferenza e il diametro di un cerchio (introdotto da William Jones nel 1706).

Oltre alla famosa identità di Euler è ricordato per il suo lavoro sulle serie infinite, sulla teoria dei grafi (il problema dei ponti di Königsberg è un esempio classico) e per il suo contributo alla soluzione di equazioni di quarto grado. La sua opera ha gettato le basi per molti sviluppi successivi in vari rami della matematica e continua ad essere una fonte di ispirazione per matematici di tutto il mondo.

La formula di Eulero

Torniamo all'identità di Eulero, che abbiamo già visto essere è una delle equazioni più affascinanti in matematica perché collega insieme cinque delle più importanti costanti matematiche utilizzando operazioni di base e concetti avanzati, e alla formula di Eulero.

Questa formula è un caso speciale della più generale formula di Eulero, che afferma che per ogni numero reale x, vale la seguente relazione:

e^ix = cos(x) + i sen(x)

La formula di Eulero mostra come l'esponenziale complesso e^ix possa essere rappresentato in termini delle funzioni trigonometriche seno e coseno.

L'identità di Eulero emerge ponendo x = π portando alla relazione:

e^iπ = cos(π) + i sen(π)

Poiché cos(π) = -1 e sin(π) = 0, otteniamo:

e^iπ = -1

e quindi l'identità di Eulero:

e^iπ + 1 = 0

Questa identità è sorprendente perché connette un numero trascendentale e, un numero irrazionale π, l'unità immaginaria i, lo zero (0), e l'unità (1) in un'unica, elegante equazione.

La formula di Eulero non solo dimostra una profonda relazione tra diverse aree della matematica, ma ha anche applicazioni pratiche in ingegneria, fisica, e altri campi scientifici, specialmente in contesti che coinvolgono fenomeni periodici e l'analisi dei segnali.

Perchè i logaritmi a base e sono detti naturali

I logaritmi naturali, identificati come logaritmi a base e sono definiti "naturali" non per una convenzione arbitraria, ma perché emergono spontaneamente attraverso vari principi e fenomeni naturali e matematici.

Questa "naturalità" si manifesta in diverse maniere significative.

Presenza in fenomeni naturali: I logaritmi naturali appaiono in contesti di crescita e decrescita naturale, come nella modellazione della crescita della popolazione, nel decadimento radioattivo, e nelle leggi che regolano le reazioni chimiche. Il fatto che la base e modelli così bene questi fenomeni deriva dalle sue proprietà uniche, rendendola una scelta "naturale" per queste applicazioni.

Calcolo infinitesimale: Nel campo del calcolo, la funzione esponenziale e^x è l'unica funzione che è esattamente uguale alla propria derivata. Questa proprietà rende le equazioni che coinvolgono e^x (e, per estensione, i logaritmi naturali) particolarmente eleganti e semplici da trattare, soprattutto in contesti di differenziazione e integrazione. Per esempio, la derivata di ^ln(x) è ^1/x, e l'integrale di 1/x è ln(x), dimostrando la naturalezza dei logaritmi naturali nel linguaggio del calcolo.

Semplificazione matematica: I logaritmi naturali possiedono proprietà algebriche che semplificano l'analisi matematica, come nella risoluzione di equazioni differenziali o nella somma di serie infinite. La base e facilita queste operazioni, rendendo i calcoli più diretti e intuitivi.

Universalità e applicabilità: Oltre alla matematica pura, i logaritmi naturali trovano applicazione in una vasta gamma di discipline scientifiche, dall'economia alla fisica, dove processi che esibiscono una crescita esponenziale o logaritmica sono meglio descritti utilizzando la base e. La loro presenza trasversale attesta la loro fondamentale "naturalità" nel descrivere il mondo.

Un esempio dell’uso di e : il calcolo dell’interesse composto

Il numero di eulero è alla basa del calcolo dell'interesse composto, fondamento della finanza: l'uso si basa sulla formula esponenziale e^rt , dove r è il tasso di interesse e t il tempo, mostrando come investimenti e prestiti crescano nel tempo.

La relazione tra il numero e e il calcolo dell'interesse composto emerge quando si considera la capitalizzazione continua di un interesse su un prestito o un investimento.

La formula base per calcolare l'ammontare futuro A di un investimento iniziale P con un tasso di interesse annuale r capitalizzato n volte all'anno, dopo t anni, è data da:

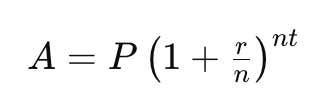
Tuttavia, se si lascia che il numero di periodi di capitalizzazione n cresca all'infinito (ovvero, se l'interesse viene calcolato e aggiunto al capitale un numero infinito di volte all'interno di un anno, o capitalizzazione continua), si arriva a una situazione in cui si applica il numero e. 

In questo caso, l'equazione si trasforma nella formula per l'interesse composto con capitalizzazione continua:

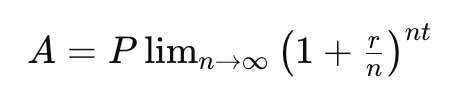
Questa espressione può essere riscritta usando la definizione di e:

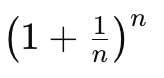
quando n tende all'infinito:

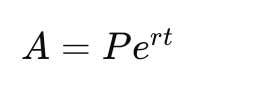
Questa formula mostra come il capitale P cresca esponenzialmente con un tasso di crescita r su un periodo di tempo t dove e è la base della crescita esponenziale.

Vediamo un esempio pratico per chiarire.

Supponiamo di avere un prestito o un investimento di 1000€ (quindi P = 1.000 €) con un tasso di interesse annuale del 5% (quindi r = 0.05) per 10 anni (t = 10). Utilizzando la formula per l'interesse composto con capitalizzazione continua, possiamo calcolare l'ammontare futuro A.

A = 1000 e^0,05x10

Calcoliamo il valore di A.