Ponte Morandi: dall’elogio dell’inaugurazione all'oltraggio della demolizione

Analisi delle critiche al progetto

Parte Prima

Nel presente articolo, dopo aver inquadrato brevemente alcuni aspetti salienti dell’opera, verranno illustrate e commentate le critiche più importanti e gravi che, a seguito del crollo parziale avvenuto il 14 Agosto 2018, alcuni colleghi hanno mosso al progetto del famoso ponte di Genova. Essendo tanti gli argomenti, il lavoro verrà suddiviso in più parti.

Considerato l’effetto che queste critiche hanno avuto sull’opinione pubblica, prima di ogni altra cosa risultano necessari alcuni chiarimenti. E auspico che altri colleghi collaborino a far questo, ciascuno per le proprie competenze e possibilità.

Non si riporteranno nel seguito né disegni del ponte, né particolari costruttivi. Si riporteranno solo elaborazioni del sottoscritto.

Il concepimento del Ponte sul Polcevera e la scelta del CAP

L’opera nasce nei primi anni ’60, e viene terminata nel ’67, in un contesto urbano completamente edificato.

Morandi opta per una struttura in cemento armato precompresso. All’epoca il CAP era preferito quasi sempre all’acciaio (anche dalle commissioni giudicatrici dei progetti); ciò derivava da esigenze di minimizzare i costi, ottenere massima durabilità e minima manutenzione. Per cui, in questa scelta, non vi è nulla di contraddittorio.

Per approfondire sulla progettazione dell'opera LEGGI L'ARTICOLO DI RICCARDO MORANDI SCRITTO NEL '67 COI DETTAGLI COSTRUTTIVI.

Lo schema statico della struttura strallata

Ognuna delle tre strutture può essere definita “strallata” per la presenza, in effetti, dei quattro grandi tiranti in CA (due per lato). In questo modo si ottiene una “travata naturalmente precompressa”, per l’effetto di compressione naturale dei 4 grandi stralli, derivata solo dalla configurazione geometrica.

Partendo dall’analisi di ciascuna struttura (le cosiddette “Pile” 9-10 e 11) si osserva che la sua semplicità è solo apparente in quanto costituita da un sistema tridimensionale di travature, molte delle quali rastremate.

L’impalcato viario

Si tratta di un cassone in cemento armato pluri-cellulare, di larghezza pari a 18 metri (due corsie per ogni senso di marcia + 2 marciapiedi) e altezza pari a 4,5 metri, con pareti di spessore variabile nelle varie sezioni longitudinali. Semplificando al massimo, l’impalcato può considerarsi longitudinalmente su quattro appoggi “fissi” rispetto ai movimenti verticali, in virtù dell’alta rigidezza estensionale degli stralli. Quindi, immaginando in prima battuta un modello “piano”, esso sarebbe due volte iperstatico. In realtà la travata è solidarizzata ai pilastri centrali, quindi il sistema ha un maggior numero di incognite iperstatiche.

I tiranti in CA (stralli)

La loro realizzazione, assolutamente unica, è tale da poter trascurare la loro rigidezza estensionale rispetto all’impalcato a cassone. Ciò viene ottenuto tramite l’utilizzo di cavi principali portanti (trefoli da CAP da ½ “), tesati fino a rendere orizzontale l’impalcato quando sottoposto ai carichi permanenti. Si osserva subito che tali cavi, essendo lunghi circa 84 metri, non avrebbero mai avuto rigidezza sufficiente per poter fornire vincoli “fissi” alla travata. Pertanto Morandi li inguaina in un getto in calcestruzzo, quest’ultimo precompresso tramite ulteriori cavi (secondari), al fine di aumentare la rigidezza estensionale dello strallo e contemporaneamente proteggere i trefoli principali dalla corrosione.

Come detto, si tratta di stralli lunghi circa 84 m, inclinati con pendenza del 64% (circa 33°), da gettare in opera, ad altezze notevoli.

Dal punto di vista del calcolo, si vede subito che le fasi di verifica dei cavi portanti sono più d’una, in quanto i cavi si troveranno a resistere “per forma” e in funzione del carico applicato, secondo la catenaria, ma anche allungandosi e interagendo con l’impalcato. Non dimentichiamo che il problema all’epoca poteva essere affrontato e risolto solo per via analitica. Oggi è possibile risolverlo per via numerica con software appositi, disponendo di elementi finiti “fune”, o “cavo”, con formulazione in grandi spostamenti, e un solutore non lineare.

Si vede allora che, pensando per semplicità a un’unica fune di area equivalente ai 352 cavi principali da 0.93 cm^2, pari a una sezione resistente di 327 cm², fissata in sommità e assoggettata in basso al peso dell’impalcato in quella fase (circa 910 t) con spostamento orizzontale impedito (per presenza dell’impalcato), si ha quanto segue:

Fase (1): Dapprima il solo peso proprio del cavo, tesato per sopportare il peso dell’impalcato (circa 910 ton) che trova la propria configurazione d’equilibrio con una freccia massima di circa 11 cm; le tensioni nel cavo variano di poco (circa 5170 kg/cm²). Vedere immagini seguenti

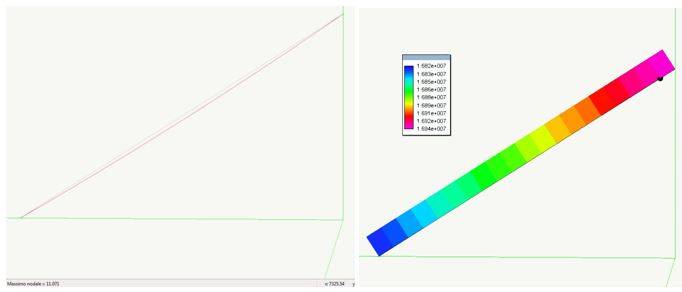
Fase (2): si aggiunge il peso del getto esterno (guaina in CLS sez. 100x120 cm – pp=3.000 kg/m), che graverà sui cavi principali già tesati: risolvendo si ha che la freccia passa a 116 cm, e le tensioni nei cavi (massimo sull’antenna) passano a 6460 kg/cm². Vedere immagini seguenti

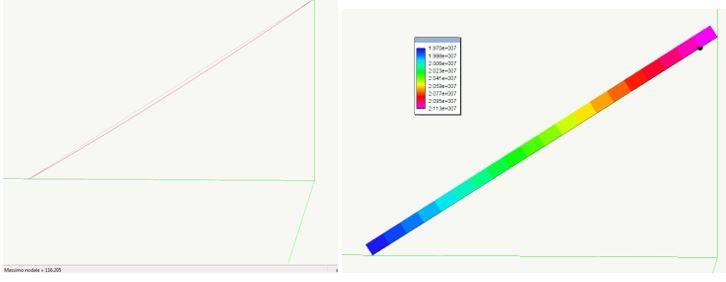
Ovviamente le tensioni aumenteranno ancora nelle fasi successive, aggiungendo i pesi permanenti e i carichi variabili, con massimo sempre in sommità. Si tratta tuttavia di cavi ad alta resistenza (oltre i 17.000 kg/cm²). 

Fase (3): La guaina esterna viene precompressa. In questa fase si tratta di studiare la stabilità di un’asta, già in configurazione curva, soggetta a carico di punta ma stabilizzata dai cavi interni tesi.

Fase (4): vengono iniettati i cavi principali, al fine di solidarizzarli alla guaina esterna, creando lo strallo “finale” ideato da Morandi.

Notiamo inoltre che, con i carichi variabili da traffico, il tirante “omogeneizzato” lavora in decompressione. Quindi la sua rigidezza estensionale “K” vale: K=F/L ; ponendo F=1 si ha K= EA/L. Essendo la sezione pari a 100 x 120 cm, e avendo il CLS un modulo elastico di circa 350.000 kg/cm^2, si ottiene che K vale = 350.000 * 12.000 / 8.400 = 500 t/cm.

I cavi primari invece, senza la guaina in CLS, avrebbero avuto la rigidezza K’ = 2.100.000*327/8.400 = 81,7 t/cm, cioè meno di 1/10. Si vede quindi che:

• senza lo strallo omogeneizzato “alla Morandi”, anche adottando 10 ordini di stralli da 327 cm² cadauno non si sarebbe mai ottenuto un vincolamento assimilabile al fisso per il cassone; 
• la variazione tensionale nei cavi primari dovuta ai carichi variabili, una volta iniettati correttamente questi ultimi, risulta trascurabile, in quanto lo strallo lavora per decompressione del CLS;
• questo corretto funzionamento del “sistema” omogeneizzato è facilmente verificabile in sede di collaudo, con misure estensimetriche sul CLS e misurando l’abbassamento totale dell’impalcato

Si può concludere che le tensioni “di lavoro” di questi elementi non superano il 50% del carico di rottura e risultano sostanzialmente insensibili ai carichi ciclici da traffico. E tutto ciò è valido fino a quando non si fessura a trazione la guaina in CLS.

Non è ben chiaro al sottoscritto come Morandi, dal punto di vista pratico-realizzativo, sia riuscito a realizzare questi stralli. Tuttavia vi sono colleghi che stanno studiando i disegni esecutivi, e altri hanno lavorato addirittura al rinforzo degli stralli dalla pila 11, per cui ci potranno in futuro fornire chiarimenti.

Sull'argomento leggi anche gli articoli

• Come e perché intervenimmo sugli stralli della pila 11 del Ponte Morandi nel 1992: intervista all'ing. Camomilla
• Dall’analisi della riparazione della Pila 11 del viadotto Polcevera all’idea del ponte moderno 

L’autorizzazione ministeriale, il Collaudo e la messa in esercizio

Il Progetto è stato elaborato in ottemperanza alle normative vigenti all’epoca, e in particolare le normative sul CA, sul CAP e sui carichi dei ponti.

Ha poi ottenuto l’autorizzazione del Consiglio superiore dei lavori Pubblici, in quanto obbligatoria all’epoca essendo una struttura in CAP. Al termine della costruzione il ponte è stato sottoposto a Collaudo statico, tramite prove di carico, in quanto obbligatorio anch’esso. So che alcuni colleghi hanno recuperato le immagini dell’epoca, con le foto della strumentazione utilizzata.

Sui contenuti delle normative suddette, e sul confronto con quelle attuali, si tornerà nel seguito. 

Il Calcolo del sistema iperstatico

Potrebbe sembrare semplice affrontare l’analisi di questa struttura, disponendo di un qualsiasi software commerciale, ma così non è.

In prima approssimazione, avendo a disposizione i carichi e le geometrie, si può partire da un’analisi elastica lineare.

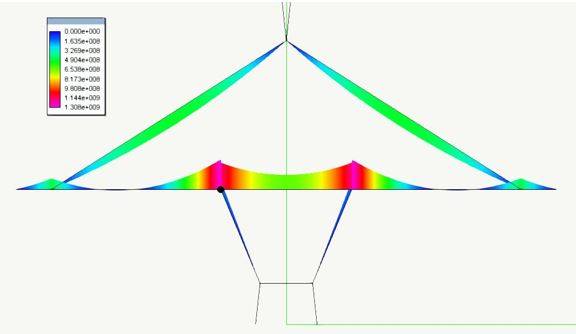
Esempio di modellazione piana del Polcevera

Ci si accorge però subito della complessità del problema, che richiede una conoscenza ingegneristica approfondita di molte tematiche. Dei tiranti si è già detto; poi abbiamo il cassone pluricellulare, iperstatico e precompresso; poi abbiamo la ripartizione trasversale dei carichi; poi abbiamo le fasi di montaggio; ecc.

Trattandosi di un progetto degli anni ‘60, ovviamente il calcolo è stato svolto con metodi manuali, per cui tutto risulta ancora più difficoltoso.

Il sistema iperstatico, immaginando i tiranti inestensibili, è stato risolto con il metodo della “Congruenza” (o delle Forze), che porta ad equazioni di congruenza del tipo [C]*{F}={α}, note come “equazioni di Muller-Breslau”, dove. Tale metodo veniva all’epoca preferito, rispetto a quello dell’Equilibrio (oggi più abituale a noi), in quanto più facilmente risolvibile “a mano”. Nelle “n” equazioni di congruenza in “n” incognite, si ha:

• [C] è la matrice di deformabilità,
• {F} è il vettore delle incognite (Forze) iperstatiche,
• {α} è il vettore dei termini noti, cioè i movimenti dovuti ai carichi esterni nella struttura resa isostatica.

I termini della matrice [C] e i termini noti possono essere calcolati applicando il Principio dei lavori virtuali. Risulta però subito evidente che, anche il semplice calcolo di un telaio piano (vedi immagine soprastante) a 8 iperstatiche (momenti), richiede un gran lavoro di calcolo di integrali del lavoro di deformazione, in quando la matrice [C], pur essendo simmetrica, è composta da 64 coefficienti. E occorre calcolarli tutti, in quanto la proprietà di simmetria serve per verificare le approssimazioni di calcolo.

Considerando , quindi, anche solo il contributo del momento (ove la struttura sia sufficientemente snella), si tratta di calcolare con il PLV parecchi integrali del tipo ∫M dφ , oppure anche ∫M*(M'/EI) dz, (ove “Z” è l’asse dell’asta considerata), prendendo in conto tutte le aste sollecitate; tenendo poi presente che le stesse sono rastremate, gli integrali si complicano per la variabilità del momento d’inerzia lungo l’asse , ma possono essere calcolati per via “discreta” con il metodo di Simpson (su questo argomento vedere ad esempio: O. Belluzzi – Scienza delle Costruzioni – Vol 2 ).

Per vedere un esempio di calcolo di una struttura con questo metodo, vedere ad esempio: Piero Pozzati – Vol 1 – pagg. 272-273, di cui si riporta uno stralcio. Per il metodo di Simpson sul calcolo discreto degli integrali si veda ad esempio : O.Belluzzi “Scienza delle Costruzioni” – Vol. 2 – pag 159.

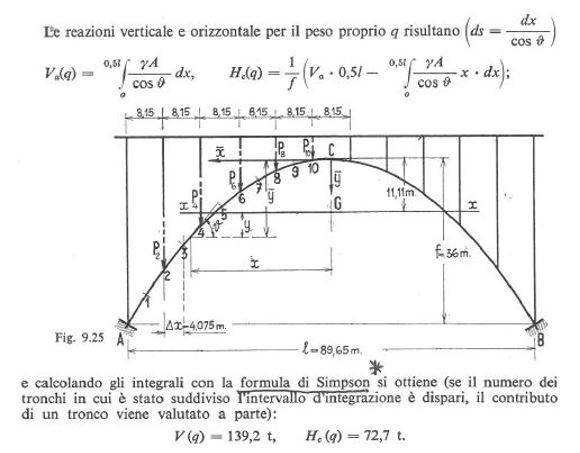
Anche i movimenti dovuti ai carichi esterni, cioè i termini noti, devono essere calcolati con il PLV. I colleghi che stanno lavorando a questi studi potranno essere molto più esaustivi, avendo disponibile il materiale originale. Si parla di un volume intero, scritto a mano, di calcoli di coefficienti di matrici.

Tutto ciò è solo per i carichi “permanenti”, strutturali e portati. Poi vi sono da calcolare le linee di influenza dei carichi variabili nelle varie sezioni notevoli (di verifica), che devono anch’esse essere calcolate a mano, ad esempio utilizzando il teorema di Land-Colonnetti, valido in campo elastico.

Poi vi sono tutte le fasi costruttive, anch’esse tutte verificate, in quanto la geometria variava da fase a fase, almeno fino all’aggancio degli stralli.

In conclusione: un progetto di questo genere, con gli strumenti dell’epoca, era alla portata di pochissimi. Ma ciò vale anche oggi, nonostante i programmi di calcolo. Oggi forse sarebbe eccessivo anche per un dottorato di ricerca, per la varietà di tematiche che tocca. E abbiamo sorvolato sul problema delle fondazioni. Un’opera, quindi, che richiede un lavoro progettuale notevolmente complesso e lungo, di altissimo livello ingegneristico. 

Le critiche al Progetto

Diverse sono state le critiche avanzate all’opera successivamente al crollo. Nel seguito verranno trattate quelle più rilevanti.

a) Carichi di progetto, vigenti all’epoca, inferiori a quelli delle norme attuali.

Com’è facile verificare, la normativa sui carichi dei ponti vigente all’epoca prevedeva dei carichi che, sostanzialmente, sono rimasti invariati anche nei decenni successivi, quando il traffico già era aumentato ai livelli che conosciamo oggi.

ESEMPIO: prendendo a riferimento le norme italiane emanate nel 1980:

- il carico di tipo “A” vale: 4.35-L/250 (t/m); quindi ponendo L = 172 m (lunghezza totale della pila 9), il carico varrebbe: 3.7 t/m. Il carico adottato da Morandi vale 4.1 t/m, che equivarrebbe ad una luce di calcolo di circa 60 m, quindi riferito circa all’interasse degli appoggi anziché ai 172 m effettivi della pila completa.

- Stessa cosa vale per le stese di Carico di tipo “B”.

- La folla sui marciapiedi vale 0.4 t/mq, che è lo stesso valore adottato da Morandi.

- Incremento dinamico Φ del carico: quello considerato da Morandi è a favore di sicurezza. Vale: 1.17-1.20 ; facendo riferimento ad un noto testo di “Costruzioni di ponti” degli anni ’80, si legge testualmente: “.. Il coefficiente dinamico Φ è normalmente inferiore a 1.4-1.5, per decrescere fino a 1 per luci superiori a 80-100 m”. Ne discende che Morandi ha considerato il coefficiente dinamico relativo alle luci intermedie, a favore di sicurezza.

Concludendo, la critica sui carichi di progetto, a mio giudizio, è completamente infondata. L’unico fatto (pare) riscontrato inerente i carichi del Polcevera è che, negli anni, sono stati aumentati i carichi permanenti. Per i variabili da traffico, invece, è aumentata la frequenza ma non l’entità, ma si è già visto che gli stralli del Polcevera, quando “integri”, sono poco sensibili ai carichi variabili ciclici (da traffico).

...continua la lettura delle altre critiche nel pdf. 

La prima immagine dell'articolo è un'immagine di Google del viadotto Polcevera prima del crollo