Analisi dinamica e modellazione numerica: valutare la risposta strutturale dei ponti esistenti

L’articolo, suddiviso in due parti, documenta una campagna diagnostica completa su un ponte esistente in calcestruzzo armato seguita dall'analisi del comportamento dinamico sotto carichi mobili mediante l’identificazione modale operativa e la simulazione FEM. La prima parte affronta le prove non distruttive, i rilievi geometrici e le analisi sui materiali, finalizzate alla caratterizzazione meccanica e alla valutazione della durabilità. I risultati ottenuti costituiscono la base conoscitiva per la seconda parte, dedicata all’identificazione modale sperimentale e alla modellazione numerica agli elementi finiti (FEM), con lo scopo di valutare la risposta dinamica globale della struttura. Un esempio concreto di approccio integrato per la verifica della sicurezza e dell’efficienza strutturale delle infrastrutture esistenti.

  

Seconda Parte

Identificazione Dinamica Sperimentale (Analisi Modale Operativa)

Dopo la fase di indagine diagnostica, per comprendere il comportamento vibratorio globale del ponte, è stata eseguita un’identificazione dinamica sperimentale.

Questa prova non distruttiva consiste nell’analizzare le vibrazioni proprie della struttura (in condizioni di normale esercizio) e nel ricavarne i parametri modali caratteristici: frequenze naturali, forme modali e coefficienti di smorzamento.

Nel caso in studio, l’identificazione è stata condotta tramite Analisi Modale Operativa (OMA), installando una rete di accelerometri sull’impalcato e sulle pile e sfruttando le vibrazioni indotte dal normale traffico veicolare come input dinamico.

In pratica, senza interrompere l’esercizio del ponte, si sono registrate le micro-vibrazioni generate dal passaggio dei veicoli e, mediante analisi nel dominio delle frequenze, si sono estratte le principali frequenze proprie e le relative forme modali della struttura.

Il ponte è stato oggetto di n°2 campagne di indagini sperimentali volte all’identificazione dinamica sperimentale dei modi propri di vibrazione dell’impalcato. Le indagini, che hanno riguardato separatamente la carreggiata lato “monte” e lato “valle”, sono state eseguite secondo la Analisi Modale Operativa sfruttando come sorgente di eccitazione strutturale il traffico veicolare presente sull’opera.

 

  

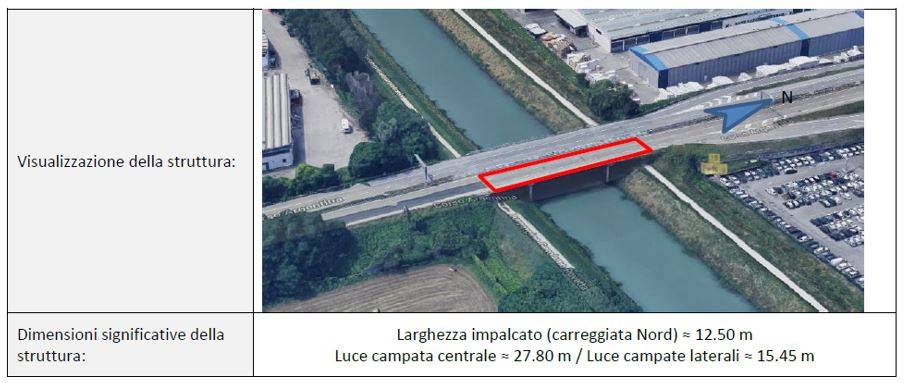
A seguire si riporta uno stralcio dei risultati ottenuti per la carreggiata Nord di valle. Mediante l’utilizzo di n°9 accelerometri sismici fissati direttamente alle strutture principali in c.a. del ponte secondo n°3 configurazioni diverse, aventi in comune alcuni punti di misura definiti come “reference”, gli sperimentatori sono stati in grado di identificare:

• n°1 forma globale flessionale (nel piano verticale) simmetrica delle due parti laterali: F = 3.62 Hz;
• n°1 forma globale flessionale di ordine superiore: F = 13.09 Hz

  

  

  

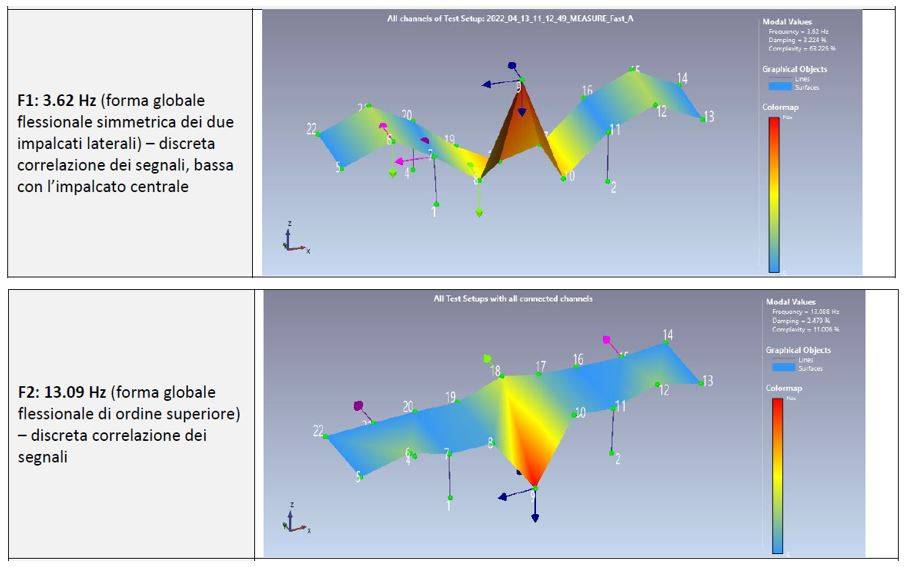
A seguire si riporta uno stralcio dei risultati ottenuti per la carreggiata Sud di valle. Mediante l’utilizzo di n°9 accelerometri sismici fissati direttamente alle strutture principali in c.a. del ponte secondo n°3 configurazioni diverse, aventi in comune alcuni punti di misura definiti come “reference”, gli sperimentatori sono stati in grado di identificare:

• n°1 forma globale flessionale (nel piano verticale) simmetrica delle due parti laterali: F = 3.40 Hz;
• n°1 forma globale flessionale di ordine superiore: F = 9.69 Hz

 

   

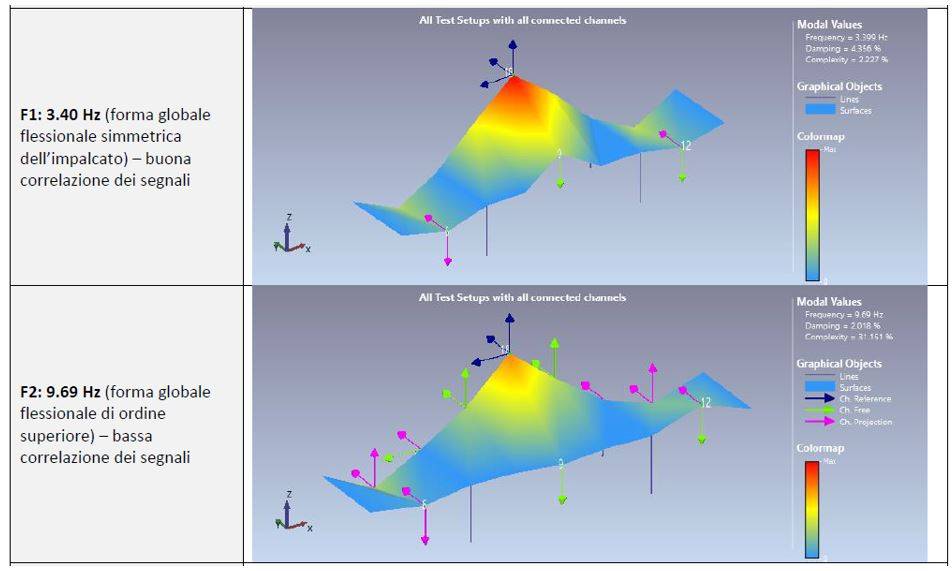
I risultati hanno evidenziato che il ponte possiede i modi fondamentali di vibrazione attesi per una struttura con due campate continue e sella Gerber centrale (schema costruttivo dell’opera).

In particolare, sono stati identificati due modi globali principali su ciascuna delle due semi-carreggiate (lato Valle e lato Monte): il primo modo flessionale verticale (simmetrico) e un secondo modo flessionale di ordine superiore.

La Tabella 1 riassume le frequenze misurate per questi modi sulle due carreggiate:

 

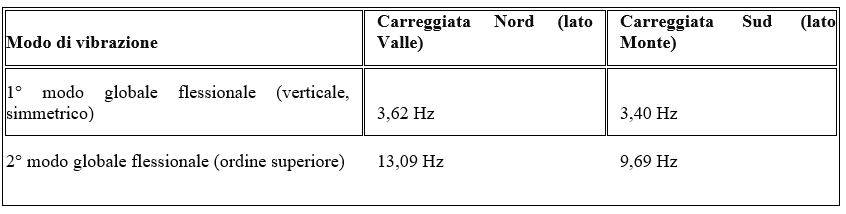
Dati ottenuti tramite OMA durante due campagne separate sulle carreggiate Nord e Sud

     

Si osserva che i modi fondamentali (primo modo) delle due carreggiate risultano sostanzialmente sovrapponibili: le frequenze sono molto vicine (3,62 Hz vs 3,40 Hz, con uno scarto di 0,22 Hz attribuibile a piccole differenze nei carichi permanenti e agli inevitabili errori sperimentali).

Ciò indica che entrambe le metà del ponte si comportano in modo analogo ed equilibrato. Le forme modali associate a questo primo modo mostrano una deformata flessionale globale dell’impalcato, coerente con quella attesa da modello (un oscillare verso il basso delle campate laterali in fase tra loro).

Le forme modali superiori identificate, pur similari nella configurazione deformativa (flessioni locali), presentano invece frequenze piuttosto diverse tra carreggiata Nord e Sud (13,09 Hz vs 9,69 Hz). Questa differenza suggerisce che tali modi possono essere influenzati da dettagli strutturali locali o condizioni di contorno leggermente diverse (ad esempio differenze nelle condizioni dei vincoli o nella distribuzione dei carichi secondari).

In ogni caso, le prime due frequenze identificate sperimentalmente sono risultate in buon accordo con quelle stimate tramite modelli di calcolo preliminari, indicando che la rigidezza globale della struttura non ha subito riduzioni anomale. Questo è un aspetto positivo che segnala l’assenza di gravi danneggiamenti interni (ad esempio fessurazioni passanti in sezioni critiche o cedimenti nei vincoli).

L’analisi dinamica ha anche permesso di stimare i coefficienti di smorzamento strutturale del ponte, risultati intorno al 2–3% del critico per i modi principali: valori tipici per ponti in c.a. in buono stato. Questi dati di smorzamento sono utili per valutare la dissipazione di energia del ponte sotto carichi ciclici (come il vento o il traffico).

In sintesi, l’identificazione dinamica fornisce una sorta di “radiografia” del comportamento strutturale d’insieme: i parametri modali ottenuti rappresentano l’“impronta digitale” dinamica del ponte allo stato attuale. Eventuali variazioni future di questi parametri (in attività di monitoraggio periodico) potranno segnalare l’insorgere di problemi strutturali, fungendo da sistema di allerta precoce.

Nel caso presente, i risultati dinamici hanno confermato che il ponte, allo stato attuale, si comporta in maniera coerente con una struttura sana, senza anomalie significative.

    

Modellazione Numerica e Analisi del Comportamento Dinamico

A valle dell’identificazione dinamica sperimentale, è stato sviluppato un modello numerico agli elementi finiti (EF) della struttura, al fine di affinare la comprensione del comportamento e di effettuare simulazioni utili alla valutazione in servizio.

Il modello EF della singola carreggiata del ponte è stato realizzato con il software SAP2000®, rappresentando le travi principali e i traversi come elementi monodimensionali tipo frame e le solette come elementi bidimensionali shell. Sono stati implementati i vincoli di appoggio in corrispondenza delle spalle e pile (semplici appoggi, in accordo con le condizioni al contorno reali, dato che il ponte non ha appoggi mobili degni di nota).

Nella zona centrale, in corrispondenza delle selle Gerber (giunto interno fra le campate), le travi principali sono state modellate inserendo cerniere interne (releases) per simulare correttamente il comportamento semi discontinuo in quel punto, come da progetto originario.

  

  

  

 

    

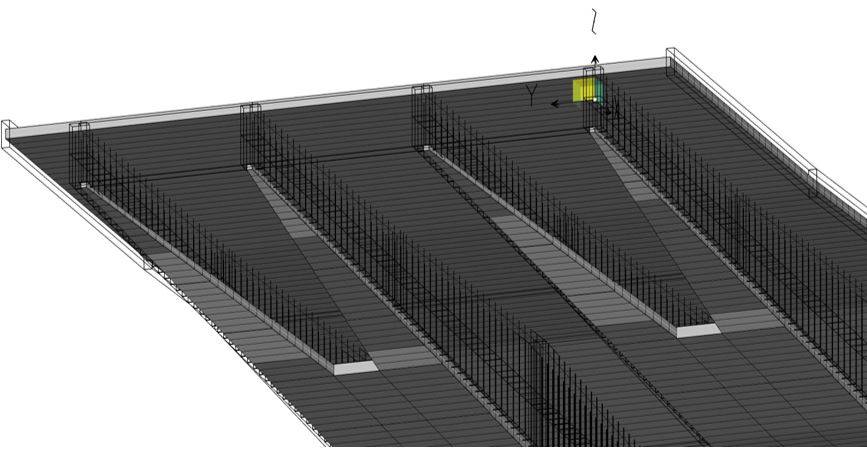
Una volta costruito, il modello è stato sottoposto ad analisi modale numerica per calcolarne i modi propri di vibrazione (frequenze e forme modali) e confrontarli con quelli ottenuti sperimentalmente.

Questo confronto ha consentito di calibrare i parametri del modello, in particolare le proprietà del materiale (calcestruzzo) in termini di rigidezza effettiva. In generale, le caratteristiche dinamiche di un ponte in c.a. dipendono da vari fattori: geometria della struttura (luci, sezione delle travi, etc.), condizioni di vincolo, carichi permanenti, peso specifico e modulo elastico del calcestruzzo, e dallo stato fessurativo (una sezione fessurata risulta meno rigida di una intatta).

Nel nostro caso, geometria, carichi e schema statico erano noti con buona approssimazione dai disegni originali e dalle indagini effettuate; la variabile principale da calibrare era dunque il modulo elastico equivalente del calcestruzzo in esercizio, tenendo conto della fessurazione.

L’analisi modale consente di calcolare, all’interno del modello agli elementi finiti, i modi propri di vibrazione della struttura rappresentata sia in termini di frequenze che di forme modali. Il confronto dei calcoli teorici con i risultati sperimentali consente di calibrare i parametri di riferimento del modello ed ottenere infine la calibrazione numerica.

In particolare, le caratteristiche dinamiche del ponte in argomento dipendono dai seguenti fattori:

• Geometria: numero e luci travi, larghezza totale, passo travi, dimensioni sezioni in c.a. delle travate e delle solette;
• Caratteristiche meccaniche calcestruzzo: peso specifico, modulo elastico
• Carichi permanenti portati
• Condizioni di vincolo.

Alcuni dei fattori citati possono essere considerati in effetti noti: la geometria dell’opera, i carichi permanenti portati (grazie alla disponibilità dei disegni originali di costruzione ed alle indagini puntuali effettuate) e le condizioni di vincolo (non sono infatti presenti apparecchi di appoggio che possono, nel tempo, variare le proprie caratteristiche meccaniche).

...CONTINUA LA LETTURA NEL PDF

---

Glossario (Acronimi e Termini Tecnici)

• OMA (Operational Modal Analysis): analisi modale operativa, tecnica per identificare i parametri modali di una struttura utilizzando solo le risposte ambientali (vibrazioni da traffico, vento, sisma minore) senza necessità di forzare la struttura con un input noto.

• Frequenza propria: frequenza alla quale la struttura tende a vibrare liberamente (modo naturale di vibrazione). Dipende dalla rigidezza e dalla massa: modalità globali di un ponte tipicamente vanno da pochi Hz (modi fondamentali) a decine di Hz (modi locali).

• Smorzamento (%): parametro che indica la dissipazione di energia nelle vibrazioni; per ponti in c.a. usualmente 1–3% (rapporto smorzamento critico).