Esoscheletri in acciaio per il retrofit di edifici in c.a.: metodologia progettuale e applicazione ad un edificio
Approfondimento sulla corretta metodologia progettuale di un esoscheletro in acciaio utilizzato per il retrofit strutturale di edifici in c.a. All'interno anche l'esempio applicativo ad un edificio.
L’utilizzo di strutture additive esterne, comunemente denominate esoscheletri, è sin dagli anni ’80 considerata una delle alternative possibili da utilizzare per retrofit sismico delle strutture esistenti in c.a. a bassa capacità dissipativa. Ne sono testimonianza i primi codici giapponesi e americani che si sono occupati di riabilitazione strutturale, nonché le molteplici applicazioni eseguite con l’uso dell’acciaio in ambito internazionale, soprattutto in zone ad alta pericolosità sismica.
L’utilizzo di tale strategia di intervento è oggigiorno ritornata di grande attualità, non solo perché è l’unica implementabile in maniera sicura senza interrompere l’utilizzo della costruzione, ma anche perché può essere efficacemente adottata, nei casi in cui si possa effettuare un ampliamento strutturale con addizione laterale di volumi, per il retrofit integrato (formale, energetico e funzionale) dell’intera costruzione.
Nel presente lavoro, viene illustrata la metodologia di progetto proposta per la concezione degli esoscheletri in acciaio come sistemi di retrofit additivo. Successivamente viene illustrata l'applicazione dei sistemi di adeguamento sismico esaminati al caso studio di un edificio in calcestruzzo armato esistente: la Scuola Primaria “Pietro Santini” di Loro Piceno in provincia di Macerata.
Metodologia di progetto
La metodologia proposta, che si inquadra nell’ambito del Metodo N2 e si basa sulle procedure formulate da Faella et al. (2004) e Ponzo et al. (2010), deve essere applicata per ciascuna delle due direzioni principali di analisi dell’edificio che si va ad investigare.
La fase preliminare relativa alla valutazione della vulnerabilità sismica della costruzione esistente è seguita dalla definizione degli obiettivi prestazionali attesi in seguito all’intervento di retrofit (Figura 1).
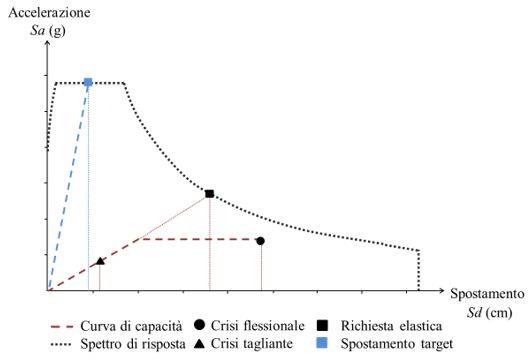
Figura 1 - Definizione dello spostamento di target.
Tale obiettivo viene individuato mediante la selezione di uno spostamento target dipendente dallo stato limite prescelto. È possibile fissare lo spostamento target nei riguardi dello stato limite di salvaguardia della vita (SLV), decidendo di mantenere la struttura esistente globalmente in campo elastico o di sfruttarne parzialmente le risorse plastiche disponibili.
Definito d*y lo spostamento di snervamento dello SDOF (oscillatore equivalente a un grado di libertà) della struttura esistente, è possibile fissare lo spostamento target Δ*tar≤d*y se si intende mantenere la struttura esistente globalmente in campo elastico.
Un’altra scelta perseguibile è quella di fissare lo spostamento target in relazione allo spostamento per il quale si verifica la prima crisi fragile d*s; pertanto è possibile fissare lo spostamento di target Δ*tar≤d*s se si intende mantenere la struttura esistente in campo elastico.
La costruzione esistente dotata di esoscheletro reagisce globalmente alle azioni orizzontali come un sistema costituito dall’accoppiamento in parallelo della costruzione esistente e dell’esoscheletro (Figura 2).
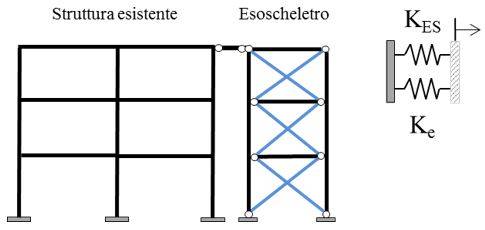
Figura 2 - Comportamento globale: accoppiamento in parallelo tra la struttura esistente e l'esoscheletro.
Assumendo come ipotesi semplificative che:
- lo spostamento di snervamento dell’esoscheletro sia coincidente con lo spostamento di snervamento della costruzione esistente;
- la massa equivalente della costruzione m* ed i coefficienti di partecipazione modale della struttura, prima e dopo l’intervento di retrofit, risultano invariati;
la rigidezza laterale globale della struttura dotata di esoscheletro Kd si calcola come segue:

dove:
Δ*tar è lo spostamento target;
F*e è la forza elastica corrispondente allo spostamento target Δ*tar;
m* è la massa equivalente del sistema SDOF;
SADRS è l’accelerazione spettrale elastica.
Poiché la costruzione esistente dotata di esoscheletro reagisce globalmente alle azioni orizzontali come un sistema in parallelo, la rigidezza laterale globale dell’esoscheletro Ke può essere calcolata mediante la seguente equazione:
Ke=Kd -KES
essendo KES la rigidezza della struttura esistente.
La rigidezza laterale globale dell’esoscheletro è distribuita successivamente a ciascun livello della costruzione.
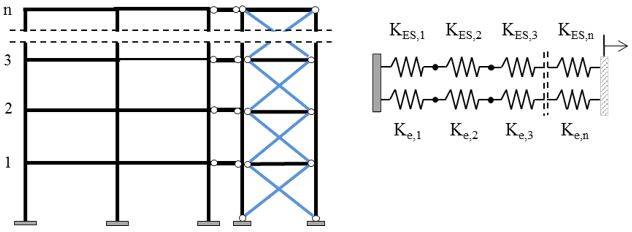
Figura 3 - Accoppiamento tra la struttura esistente e l'esoscheletro.
La distribuzione (Figura 3) viene effettuata in maniera proporzionale al fattore di sovra-rigidezza globale, r, definito come il rapporto tra la rigidezza laterale globale dell’esoscheletro ΔK e la rigidezza laterale globale della struttura allo stato di fatto KES:
r = ΔK/KES
La rigidezza dell’esoscheletro al livello i-esimo Ke,i si calcola in maniera proporzionale al fattore di sovra-rigidezza globale r:
Ke,i = r ∙ KES,i
essendo KES,i la rigidezza del livello i-esimo della struttura allo stato di fatto.
La suddetta distribuzione delle rigidezze di piano è da intendersi come soluzione di primo tentativo, poiché, essendo le rigidezze a ciascun livello proporzionali ad r, questa conserva i caratteri di regolarità della struttura esistente.
È possibile infatti applicare una procedura iterativa di regolarizzazione delle rigidezze ai diversi livelli per modificare l’iniziale distribuzione delle rigidezze allo scopo di correggere l’eventuale irregolarità strutturale in altezza dell’edificio esistente.
La procedura è stata proposta da Ponzo et al. (2010) e consente di regolarizzare in elevazione la struttura dotata di esoscheletri secondo i criteri definiti al Cap. 7 delle Norme Tecniche per le Costruzioni NTC 2018, in cui si definisce regolare la struttura la cui rigidezza, da un piano a quello sovrastante, non si riduce più del 30% e non aumenta più del 10%.
Pertanto, la procedura di regolarizzazione delle rigidezze ai diversi livelli della struttura si applica come segue:

dove:
j è il numero di interazioni necessarie per la convergenza, pari al massimo ad n;
Kd,ij è la rigidezza di piano della struttura dotata di esoscheletri;
Ke,i è la rigidezza di piano del sistema di esoscheletri;
KES,i è la rigidezza di piano della struttura esistente.
In caso di struttura esistente particolarmente irregolare, tale procedura può condurre ad una rigidezza laterale globale significativamente maggiore di quella strettamente necessaria. In questi casi è opportuno ridurre in maniera omogenea le rigidezze.
Si evidenzia, tuttavia, che per strutture fortemente irregolari l’applicazione del Metodo N2 risulta inappropriata; pertanto in tali casi è necessario prediligere l’applicazione di metodologie di calcolo maggiormente pertinenti.
La rigidezza laterale di piano dell’esoscheletro così calcolata va quindi suddivisa tra gli elementi resistenti presenti. La distribuzione di primo tentativo consiste nel dividere omogeneamente la rigidezza di piano tra gli elementi presenti:
Ke,ik =Ke,i / m
dove:
Ke,ik è la rigidezza laterale del k-esimo esoscheletro al piano i-esimo;
Ke,i è la rigidezza di piano del sistema di esoscheletri;
m è il numero di esoscheletri presenti.
Al fine di correggere le eventuali irregolarità in pianta della struttura esistente, è possibile assegnare in maniera opportuna la percentuale di rigidezza laterale di piano a ciascun elemento resistente mediante un coefficiente di distribuzione pk (Figura 4):
Ke,ik = pk ∙ Ke,i
Può risultare utile a tal fine effettuare la distribuzione al fine di far coincidere il centro di rigidezza laterale di piano con il centro di massa di piano. Pertanto, considerando la distanza dal centro di massa di piano M di ciascun elemento resistente de,ik, occorrerà assegnare iterativamente i coefficienti pk al fine di ottenere:
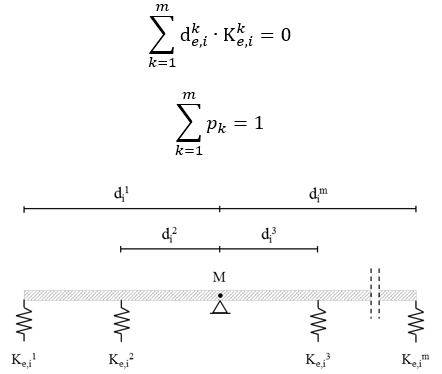
Figura 4 – Distribuzione della rigidezza di piano agli elementi resistenti.
... l'ARTICOLO CONTINUA con l'applicazione ad un caso studio: la Scuola Primaria "Pietro Santini" .
Scarica il PDF con l'articolo integrale, scaricabile previa registrazione.
Speciale Esoscheletri
Il presente articolo fa parte di una serie di contributi a firma di docenti dell'Univeristà di Napoli ed esperti (Prof. Ing. Raffaele Landolfo, Prof. Ing. Gianmaria Di Lorenzo,Prof. Ing. Antonio Formisano, Arch. Eleonora Colacurcio, Arch. Agustina Di Filippo), sul tema degli Esosceletri e in particolare sul loro uso negli interventi di retrofit sismico di edifici esistenti in calcestruzzo armato.
- Esoscheletri in acciaio per il retrofit strutturale di edifici esistenti in c.a.: stato dell'arte e definizioni
- Esoscheletri in acciaio per il retrofit strutturale di edifici esistenti in c.a.: concept strutturale e applicazioni
- Esoscheletri in acciaio per il retrofit strutturale di edifici esistenti in c.a.: metodologia progettuale e applicazione ad un edificio esistente
Costruzioni Metalliche
Le costruzioni metalliche rappresentano una scelta strategica per strutture leggere, sicure, resistenti e sostenibili. Scopri su INGENIO tecniche, norme e soluzioni per progettare con l’acciaio.

Esoscheletro
Gli esoscheletri sono al centro dell’innovazione edilizia: dispositivi per l’ergonomia dei lavoratori e sistemi strutturali esterni per edifici resilienti e sostenibili. Scopri gli approfondimenti su INGENIO.

Ingegneria Strutturale
L’ingegneria strutturale garantisce sicurezza e durabilità alle costruzioni. Scopri su INGENIO materiali, norme, tecnologie e soluzioni per progettare, rinforzare e monitorare strutture nuove ed esistenti.

Miglioramento sismico
Area di Ingenio dedicata tema degli interventi di miglioramento sismico delle strutture: normativa vigente, modalità e tecnologie di intervento nonché casi applicativi

Rinforzi Strutturali
News e approfondimenti su tutto quello che riguarda il rinforzo delle strutture: dalla modellazione e progettazione degli interventi, alla normativa, alla descrizione di soluzioni tecniche e particolari costruttivi.

Sismica
Tutti gli articoli pubblicati da Ingenio nell’ambito della sismologia e dell’ingegneria sismica.
Condividi su: Facebook LinkedIn Twitter WhatsApp


