Analisi di pushover su edifici esistenti in muratura

Strutture in muratura

La maggior parte delle strutture esistenti in Italia presenta pareti portanti in muratura. Come si può estrarre dai dati ISTAT [7], ad esempio, per quanto riguarda gli edifici residenziali, il 57% di essi ha struttura in muratura, di cui la maggior parte costruiti in epoche precedenti al 1980.

Considerando inoltre che l’Italia ha una pericolosità sismica medio-alta e una vulnerabilità molto elevata [12], si può dedurre quanto sia importante eseguire miglioramenti (ovvero migliorare la risposta sismica di un edificio esistente) o adeguamenti (ovvero raggiungere il livello di sicurezza rispetto all’azione di un sisma richiesto dalla normativa per le nuove costruzioni) [1] sul costruito italiano.

Interventi su edifici esistenti in muratura: cosa prevede la normativa italiana

È estremamente complicato definire la legge costitutiva per vecchie murature, siccome non si può trovare omogeneità ed è difficile determinare tutti i danni provocati dall’uomo durante la storia dell’edificio [6].
Nelle normative italiane si descrivono dei metodi per poter agevolare lo studio di strutture esistenti.

Come descritto nei paragrafi §8 Costruzioni esistenti delle NTC2018 [11] e delle Istruzioni per le NTC [8], è necessario eseguire un’analisi storico-critica, rilievi geometrici-strutturali, analizzando i collegamenti e le possibili discontinuità, e prove in situ o in laboratorio sui materiali, per poter eseguire la caratterizzazione meccanica del materiale.

A seguito degli approfondimenti effettuati, si definiscono quindi i livelli di conoscenza con i rispettivi fattori di confidenza, che sono utilizzati per la riduzione dei valori dei parametri meccanici dei materiali.

Si riporta l’estratto dalle Istruzioni per le NTC [8]:

LC1: si intende raggiunto quando siano stati effettuati, come minimo, l’analisi storico-critica commisurata al livello considerato, con riferimento al § C8.5.1, il rilievo geometrico completo e indagini limitate sui dettagli costruttivi, con riferimento al § C8.5.2, prove limitate sulle caratteristiche meccaniche dei materiali, con riferimento al § C8.5.3; il corrispondente fattore di confidenza è FC=1,35 (nel caso di costruzioni di acciaio, se il livello di conoscenza non è LC2 solo a causa di una non estesa conoscenza sulle proprietà dei materiali, il fattore di confidenza può essere ridotto, giustificandolo con opportune considerazioni anche sulla base dell’epoca di costruzione);

LC2: si intende raggiunto quando siano stati effettuati, come minimo, l’analisi storico-critica commisurata al livello considerato, con riferimento al § C8.5.1, il rilievo geometrico completo e indagini estese sui dettagli costruttivi, con riferimento al § C8.5.2, prove estese sulle caratteristiche meccaniche dei materiali, con riferimento al § C8.5.3; il corrispondente fattore di confidenza è FC=1,2 (nel caso di costruzioni di acciaio, se il livello di conoscenza non è LC3 solo a causa di una non esaustiva conoscenza sulle proprietà dei materiali, il fattore di confidenza può essere ridotto, giustificandolo con opportune considerazioni anche sulla base dell’epoca di costruzione);

LC3: si intende raggiunto quando siano stati effettuati l’analisi storico-critica commisurata al livello considerato, come descritta al § C8.5.1, il rilievo geometrico, completo ed accurato in ogni sua parte, e indagini esaustive sui dettagli costruttivi, come descritto al § C8.5.2, prove esaustive sulle caratteristiche meccaniche dei materiali, come indicato al § C8.5.3; il corrispondente fattore di confidenza è FC=1 (da applicarsi limitatamente ai valori di quei parametri per i quali sono state eseguite le prove e le indagini su citate, mentre per gli altri parametri meccanici il valore di FC è definito coerentemente con le corrispondenti prove limitate o estese eseguite).

Una volta ottenute le caratteristiche della struttura, è importante decidere che tipo di analisi globale usare per verificare la struttura all’azione sismica.

Nel capitolo §7.3 [11] vengono proposti i diversi metodi.

L’analisi lineare o non lineare, dove in quest’ultima si tiene conto delle non linearità di materiale e geometriche; e l’analisi dinamica o statica, dipendendo dal fatto che l’equilibrio sia trattato dinamicamente o staticamente.

In questo articolo viene analizzata nel dettaglio l’analisi statica non lineare, chiamata anche analisi di pushover, applicata su edifici in muratura esistenti, come metodo per la valutazione della capacità di edifici.

L’analisi statica non lineare (analisi pushover)

Questa viene definita nelle NTC [11] come scritto di seguito:

L’analisi non lineare statica richiede che al sistema strutturale reale sia associato un sistema strutturale equivalente non lineare.

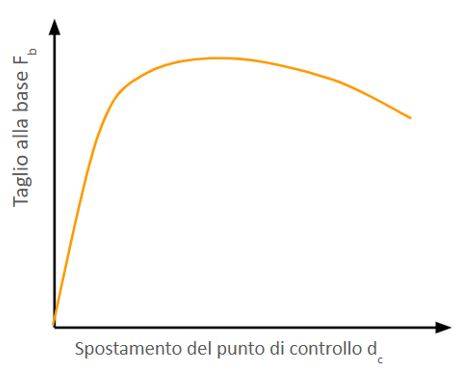
Nel caso in cui il sistema equivalente sia ad un grado di libertà, a detto sistema strutturale equivalente si applicano i carichi gravitazionali e, per la direzione considerata dell’azione sismica, in corrispondenza degli orizzontamenti della costruzione, forze orizzontali proporzionali alle forze d’inerzia aventi risultante (taglio alla base) Fb. Tali forze sono scalate in modo da far crescere monotonamente, sia in direzione positiva che negativa e fino al raggiungimento delle condizioni di collasso locale o globale, lo spostamento orizzontale dc di un punto di controllo coincidente con il centro di massa dell’ultimo livello della costruzione (sono esclusi eventuali torrini). Il diagramma Fb – dc rappresenta la curva di capacità della struttura.

L’analisi di pushover è una procedura iterativa ed è quindi condotta mantenendo costanti i carichi gravitazionali e incrementando gradualmente le forze orizzontali applicate alle masse, simulando le forze inerziali derivanti dall’azione sismica; grazie a questo metodo, che considera la non linearità del materiale, si riesce a descrivere l’origine e l’evoluzione dei meccanismi plastici all’interno del sistema strutturale [5].

La norma inoltre dice che si devono considerare due distribuzioni di forze orizzontali di tipo inerziale: le distribuzioni principali (Gruppo 1) e quelle secondarie (Gruppo 2). Il primo gruppo ha una distribuzione che deriva dall’analisi dinamica lineare per un numero di modi di vibrare sufficienti ad eccitare almeno l’85% della massa; il secondo gruppo potrebbe derivare dall’andamento uniforme di accelerazioni lungo l’altezza della costruzione.

Grazie a questa analisi si riesce a determinare la curva di capacità della struttura (Fig. 1), espressa dalla relazione Fb-dc, in cui Fb è il taglio alla base e dc è lo spostamento del punto di controllo (generalmente il centro di massa dell’ultimo orizzontamento), la curva misura la capacità del sistema strutturale di deformarsi sotto l’effetto dei carichi orizzontali, quindi misura la duttilità strutturale. Per ogni stato limite considerato, si confronta la curva di capacità e la domanda di spostamento, così da determinare il livello di prestazione.

Inoltre, quando la struttura non è simmetrica, per ciascuna direzione (x e y nel piano), devono essere eseguite due analisi distinte, applicando l’azione sismica in entrambi i possibili versi (+x, -x, +y, -y), così da valutare tutti i possibili metodi di collasso.

Dalla curva di capacità della struttura, si ricava la curva di un sistema equivalente ad un grado di libertà, scalando la forza e lo spostamento per un “fattore di partecipazione modale”; poi si riesce ad ottenere una curva bilineare, come descritto nel paragrafo §C7.3.4 [8] (Fig. 2).

È questa la curva che si deve confrontare con la domanda, ovvero lo spostamento richiesto dall’azione sismica di progetto.

Il comportamento post-elastico della struttura viene modellato attraverso l’utilizzo di cerniere plastiche, queste cerniere simulano il comportamento non-lineare.

Si tratta di una semplificazione, infatti la cerniera si comporta da incastro fino a che il momento sollecitante è inferiore al momento resistente, e poi per ogni incremento del momento sollecitante, la cerniera plastica esibisce una rotazione (Fig. 3).

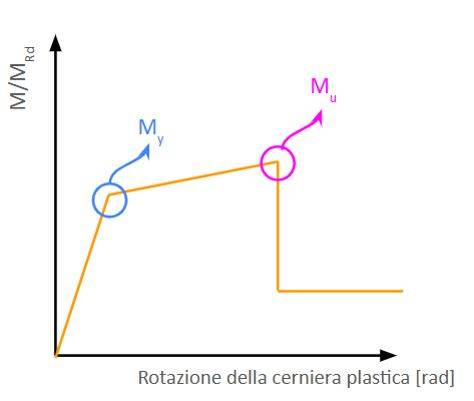
L’analisi di pushover individua quindi in ogni step di calcolo lo spostamento del punto di controllo, aggiornando iterativamente il modello con tutte le cerniere plastiche presenti nei punti in cui la struttura sta plasticizzando.

Metodo del telaio equivalente

In letteratura esistono diversi metodi di modellazione per studiare le strutture in muratura.

Le due grandi famiglie sono da una parte i modelli ad elementi finiti e dall’altra i modelli semplificati.

I modelli ad elementi richiedono molto più tempo di modellazione e più tempo per il calcolo, mentre quelli semplificati operano nell’ambito della macro-modellazione e riducono entrambe le attività [13].

In una struttura in muratura esistono due elementi resistenti: i maschi murari, ovvero quegli elementi verticali che vanno dalle fondazioni fino in sommità, e le fasce di piano, quegli elementi orizzontali che collegano due maschi murari (Fig. 4).

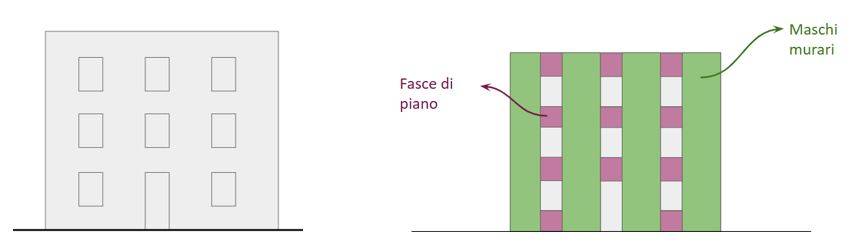
I metodi semplificati si basano sull’individuazione di questi elementi principali.
Ad esempio, il metodo POR, che considera un singolo piano per volta, ipotizza le fasce di piano come infinitamente rigide e resistenti, mentre come meccanismo di rottura la fessurazione diagonale dei maschi murari.

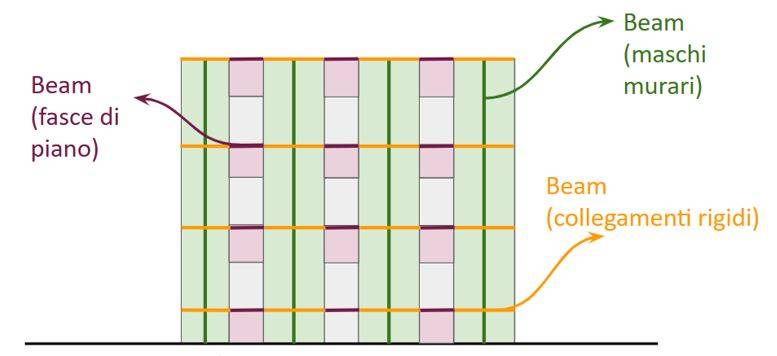
Invece, il metodo del telaio equivalente [2], metodo approfondito in questo articolo, schematizza la struttura in muratura come un telaio.

Questo metodo EFM (Equivalent Frame Model) considera i maschi murari e le fasce di piano come pilastri o travi con deformazione a taglio, collegate alle intersezioni con nodi infinitamente rigidi, così da riprodurre l’elevata rigidezza e resistenza dei pannelli in intersezione tra maschi e fasce (Fig. 5).

...CONTINUA LA LETTURA NEL PDF.

All'interno un esempio applicativo di modellazione.