La pericolosità sismica secondo le NTC e le conseguenze sull’ingegneria sismica

Dall’entrata in vigore della normativa italiana NTC2008, la cosiddetta “pericolosità sismica” dei vari siti del nostro territorio è stata trattata su base statistica. Il modello adottato, chiamato MPS04, è stato elaborato da INGV nei primi anni 2000.

Su questo modello dell’azione sismica non c’è mai stato molto dibattito fra gli ingegneri. Quasi non se ne parla (a parte qualche caso isolato) nei corsi universitari di ingegneria sismica; i seminari per ingegneri sono rarissimi; manca anche il materiale di discussione.

Ci sono però state, e ci sono, tante polemiche, in particolare sugli spettri adottati per l’azione sismica, in quanto alcuni sostengono che le azioni conseguenti siano sotto-stimate. Questo modo di ragionare, un tanto al chilo, che non spiega i motivi e non propone alternative, non può essere accettato. Allora, dopo anni di (mia) colpevole trascuratezza, ho deciso di riordinare il materiale in mio possesso e di metterlo a disposizione di tutti i colleghi, sperando possa essere utile per avviare poi un dibattito serio, basato su dati, e non su opinioni più o meno fantasiose.

Si tratta ovviamente, nella prima parte, di una trattazione ridotta all’osso, anche per la mia limitata conoscenza degli argomenti, e solo per fare emergere i punti chiave dei modelli adottati. Poi nella parte conclusiva traggo alcune prime osservazioni, commenti e spunti di riflessione che mi auguro possano essere raccolti dai colleghi che trattano la materia.

Descrizione del modello statistico adottato

La scelta di individuare l’azione sismica di progetto a partire da mappe pericolosità basate su un modello probabilistico, per le norme italiane e per noi tutti è stata una specie di rivoluzione a cui, forse, come ingegneri non ci siamo ancora completamente abituati.

Come per ogni modello della realtà fisica, ci sono vantaggi e svantaggi, problematiche, rischi applicativi, ma anche ampi margini per futuri sviluppi.

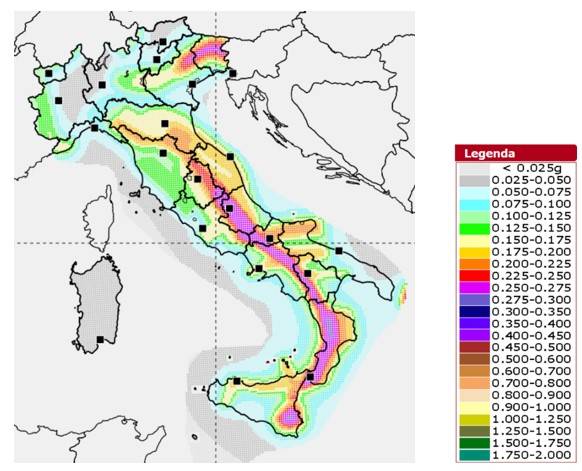
Nel modello MPS04 il parametro prescelto per individuare la pericolosità è l’accelerazione di picco al suolo “a_g”, su suolo rigido, associata a una forma spettrale (quindi in realtà una terna: a_g, F₀, T_c).

Nel seguito si analizzerà il modello statistico che sta alla base delle mappe MPS04.

Il processo sismogenetico che genera gli eventi è stato considerato di tipo stocastico poissoniano. Quindi si assume quanto segue:

• gli eventi sono indipendenti fra loro (non esistono dipendenze fra i vari eventi);
• non esistono eventi simultanei;
• il processo è stazionario, quindi qualsiasi evento è indipendente dall’istante in cui avviene;
• la distribuzione degli eventi è poissoniano.

Queste ipotesi, che definiscono il processo stocastico poissoniano, ovviamente nella realtà non sono esattamente aderenti al fenomeno, ma il modello ha una sua attendibilità e ha il vantaggio della semplicità.

In particolare, esso è governato da un solo parametro: λ, che rappresenta il numero medio di eventi in un certo arco di tempo Δt. Questo numero è alla base di tutta l’elaborazione statistica.

Primo problema affrontato: stabilire il numero λ di eventi (nel caso specifico sono quelli che superano una certa soglia di a_g), che possono avvenire in un certo sito in un certa finestra temporale Δt, ad esempio 50 anni. Quindi λ=N/Δt, rappresenta una frequenza media. L'inverso, 1/λ ,è il tempo di ritorno T, ed è sempre un dato medio.

Esempio: sappiamo che alcuni tipi di eventi avvengono 3 volte in 100 anni:

allora: λ = 3/100=0.03 ===> Tr = 33 anni

La distribuzione di probabilità nel modello di Poisson

Il modello di Poisson ha una sola variabile: N, che rappresenta il numero medio di eventi.

La probabilità P(n) associata a un numero n di eventi (dove “n” è numero naturale, compreso lo zero), fissato il numero medio è N, vale:

Grafichiamo allora la probabilità che avvengano n eventi, rispetto a un N fissato: metto in ascisse la variabile n e in ordinate la probabilità P. Esempio: per un numero medio di eventi N =10.

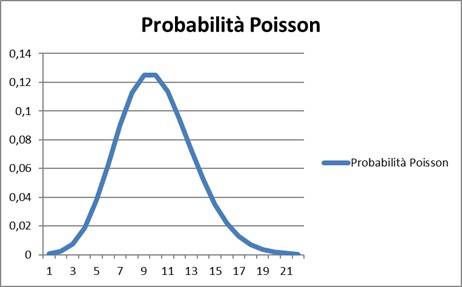
Per gli scopi della pericolosità sismica, occorre poter variare la finestra temporale Δt; quindi scrivo N come segue:

N= λ * Δt, dove λ è la frequenza degli eventi selezionati, che devo avere nota; ad esempio la ricavo da un catalogo, o con altri metodi (vedi nel seguito).

ESEMPIO: Dai dati storici so che in una finestra di 150 anni si sono verificati 5 eventi con le caratteristiche che cerco: quindi ricavo λ = 5/150= 0.033 eventi/anno.

Se la finestra temporale è Δt=50 anni, il numero di eventi N= 0.033 * 50 = 1.65

Notare le seguenti proprietà della distribuzione di Poisson:

• La somma delle probabilità vale 1 (ovvero 100%);
• il caso n=0 (nessun evento) corrisponde a una probabilità non nulla: P_N(0) = N⁰ * e^-N/ 0! = e^-N

Quindi, la probabilità che si verifichi almeno un evento (n>0) vale:

Oppure posso scrivere:

Esempio: ci interessa la probabilità che si verifichi, in un certo sito, almeno un evento avente a_g=0.01g in una finestra temporale Δt = 50 anni.

Dai dati storici so che in una finestra di 150 anni si sono verificati 5 eventi: quindi ricavo λ = 5/150 = 0.033 eventi/anno.

La probabilità che cerco vale: P=1-e^-0.033*50 = 1-0.19=0.81 (81%)

La probabilità che si verifichi almeno un evento, data dalla (2) o (3), è chiamata anche “Probabilità di eccedenza”.

Tempo di ritorno: è definito come l’inverso della frequenza λ: T_R= 1/λ Quindi nell'esempio precedente il tempo di ritorno risulta: T_R= 150/5 = 30 anni

.. CONTINUA LA LETTURA NEL PDF.

SCARICA* E LEGGI L'ARTICOLO INTEGRALE

Il pdf continua descrivendo le curve di pericolosità, le zone sismo-genetiche e i metodi per calcolare λ in un sito specifico, il metodo di Cornell e l'utilizzo dei dati dal punto di vista applicativo-ingegneristico.