1. Premessa

Nel presente lavoro si vuole illustrare una procedura operativa – utile allo strutturista – per la determinazione degli indici di robustezza strutturale in funzione della profondità di corrosione delle barre di armatura, promossa dall’azione dell’anidride carbonica - in un edificio di civile abitazione in calcestruzzo armato in cui si ipotizza il “fallimento” di una colonna in condizioni integre e in condizioni di degrado secondo diversi scenari di danno.

Nelle attuali Norme Tecniche per le Costruzioni (in seguito NTC2018), al paragrafo 2.1 viene menzionato, tra gli altri, il requisito relativo alla robustezza che devono possedere le opere e le varie tipologie strutturali (Fig. 1).

Inoltre, al paragrafo 8.2, viene riportato il termine degrado da mettere in conto nelle verifiche di sicurezza (Fig.2).

Pertanto, lo scopo di tale lavoro è stato quello di “intersecare” gli aspetti legati alla robustezza strutturale con quelli del degrado localizzato – corrosione delle barre di armatura e fessurazione del calcestruzzo - presente nelle strutture esistenti.

2. Il collasso strutturale

È opportuno distinguere il collasso sproporzionato dal collasso progressivo. Il primo si manifesta in misura maggiore rispetto ad alcuni limiti prestabiliti che definiscono la soglia tollerabile di danno, definita dalle linee guida nazionali o dalla volontà del cliente in stretta relazione con la natura dell’evento scatenante.

Tale collasso si registra se il danno finale è sproporzionato rispetto al danno iniziale provocato da una rottura locale.

Il collasso progressivo rappresenta una reazione a catena di rotture. A partire da un danno iniziale che ha interessato direttamente una porzione relativamente piccola della struttura, la rottura si propaga agli elementi vicini, che a loro volta determinano la rottura di altri elementi, con un effetto domino che può coinvolgere gran parte se non l’intera struttura.

Nello specifico, il collasso progressivo descrive la situazione in cui la struttura perde il sostegno di una o più colonne: i carichi gravitazionali vengono applicati alle travi di connessione, che agiscono come load paths alternativi e trasferiscono i carichi ai pilastri loro adiacenti.

Se gli elementi che formano questo “nuovo” load path non sono in grado di sopportare il carico aggiuntivo, il collasso si propaga, coinvolgendo con una reazione a catena l’intera struttura. Il collasso progressivo è generalmente un collasso incrementale e sproporzionato.

Nel caso invece in cui i load paths siano in grado di supportare carichi ulteriori, il collasso viene fermato e limitato agli elementi venuti a mancare. In quest’ultimo caso la struttura reagisce con diversi meccanismi di resistenza che entrano in carico con una sequenza temporale dipendente dalla tipologia strutturale e dalle modalità di collasso.

A causa della stretta dipendenza che lega il collasso sproporzionato alla natura dell’evento dannoso, il collasso progressivo non è necessariamente sproporzionato, nel caso di un fenomeno molto potente può essere accettabile anche la completa distruzione dell’edificio. Quando una colonna collassa in una struttura, il carico gravitazionale viene trasferito alle travi che si collegano ad essa e che fungono da percorso di carico alternativo nel trasferimento alle colonne adiacenti.

Se gli elementi che formano questo percorso di carico sono in grado di sopportare questa extra azione, il crollo viene arrestato e la struttura è stabile nel suo stato danneggiato (Figura 3).

   

    

Se, tuttavia, questi elementi non hanno una capacità residua sufficiente per resistere alla domanda aggiuntiva, falliscono e anche il collasso si propaga. Tale fenomeno continua fino a quando non viene rilevato un load pattern alternativo in cui la struttura offre una capacità residua sufficiente per arrestare il collasso.

I meccanismi resistenti fondamentali per conferire robustezza alla struttura sono cinque (Cormie, 2009) e sono illustrati nella Figura 4:

• azione catenaria nel telaio strutturale;
• deformazione a taglio delle strutture di trasferimento;
• azione membranale nei solai;
• azione di Vierendeel nei nodi trave colonna;
• arco di compressione nelle travi e nei solai.

Per la maggior parte delle strutture, la ridistribuzione attraverso percorsi di carico alternativi si basa sulla mobilitazione di questi comportamenti resistenti. In alcuni tipi di struttura è possibile sviluppare un'azione di sostegno a compressione in muratura (f) o simile, che può avere una notevole capacità di carico.

---

MECCANISMI RESISTENTI

   

    

    

   

    

---

Figura 4 - Schematizzazione dei possibili meccanismi di resistenza che si generano a seguito del collasso di una colonna (Cormie 2009, Arup et.al)

Per strutture tipiche in calcestruzzo armato a telaio in ambo le direzioni in presenza di tamponature, una possibile sequenza dei meccanismi resistenti all’aumentare delle deformazioni strutturali nella zona di collasso e limitrofe può essere la seguente:

1. Resistenza a compressione delle tamponature tramite la formazione di meccanismi a puntone;
2. Resistenza a flessione e taglio delle travi in piccoli spostamenti;
3. Resistenza Vierendeel, dovuta all’azione del momento flettente nelle connessioni trave-colonna;
4. Resistenza per azione ad arco in travi e solette con la formazione di bielle di calcestruzzo non fessurato in moderati spostamenti;
5. Resistenza per azione a catenaria delle travi in grandi spostamenti che vede un’azione di trazione contrapposta rispetto al nodo su cui insisteva la colonna o parete crollata;
6. Resistenza per azione membranale in grandi spostamenti degli impalcati di solaio.

    

3. I Modelli di degrado

Scopo del presente paragrafo è quello di illustrare, sinteticamente, i modelli di degrado riconosciuti dalla letteratura scientifica internazionale (per approfondimenti si rimanda alle citazioni riportate in bibliografia):

1. Modello di corrosione uniforme: noto il parametro di danno δ globale per corrosione in un certo istante per un generico elemento della struttura, determinare i parametri di danno locale che riguardano il materiale acciaio e calcestruzzo. Tali parametri riguarderanno:
2. l’acciaio con la riduzione di: area resistente delle barre, resistenza allo snervamento e ultimo del materiale, duttilità e aderenza;
3. calcestruzzo con la riduzione di: resistenza a compressione della zona degradata;
4. Modello di corrosione localizzata: noto il parametro di danno δ globale per corrosione in un certo istante per un generico elemento della struttura e il fattore di pitting R per la corrosione localizzata, determinare i parametri di danno locale che riguardano il materiale acciaio e calcestruzzo. Tali parametri sono gli stessi sopra riportati anche se valutati in maniera diversa.
5. Evoluzione temporale del degrado: la corrosione evolve con una sua velocità nota e variabile nel tempo in funzione dell’ambiente esterno e di altri fattori.

L’implementazione statica dei modelli di cui ai punti a e b ci permetteranno di valutare la capacità portante di strutture in c.a. soggette ad un certo livello di degrado in condizioni sismiche.

Indice di danno

Si utilizzerà come parametro di danneggiamento globale dal quale far dipendere gli altri indici di danno, il rapporto tra la penetrazione raggiunta dalla corrosione ed il diametro iniziale delle barre.

D₀ : δ = x/D₀

   

    

4. Metodi di analisi

L'analisi del collasso progressivo verticale di una struttura viene generalmente eseguita tramite il metodo ALP (Alternative Load Path), ovvero la rimozione istantanea di uno o più elementi portanti primari e quindi analizzare la capacità residua della struttura di assorbire il danno in assenza degli elementi collassati. In letteratura per la valutazione della propensione al collasso progressivo delle strutture, al fine di stimare un indice di robustezza, vengono proposti quattro metodi di analisi:

• Analisi statica lineare e non lineare;

• Analisi dinamica lineare e non lineare o dinamica incrementale;

La procedura di analisi statica lineare è eseguita utilizzando una combinazione amplificata di carichi di servizio, applicata staticamente e la risposta viene valutata dai rapporti domanda/capacità degli elementi strutturali in termini di forza o spostamenti DCR.

Ma ciò è limitato a strutture relativamente semplici in cui sia gli effetti non lineari che dinamici della risposta possono essere previsti in modo semplice e intuitivo. Le procedure di analisi dinamica lineare o non lineare, in particolare dinamica non lineare, sebbene la loro precisione sia molto più alta, di solito sono eseguite in casi eccezionali data la complessità.

La statica non lineare o push-down è il metodo di analisi più utilizzato ed implica un aumento graduale dei carichi verticali amplificati (di un fattore generalmente pari a 2.0), fino al raggiungimento del massimo carico amplificato o al collasso della struttura.

   

Analisi statica e/o dinamica lineare (ASL-ADL)

Le linee guida più recenti riguardo alla progettazione contro il rischio di collasso progressivo e le UFC 4-023-03 pubblicate il 14 Luglio 2009 e revisionate a Novembre del 2016.

Tale documento fornisce le linee guida per una progettazione mirata a minimizzare il rischio di collasso progressivo nelle strutture che possono essere soggette ad azioni di natura eccezionale.

La sua applicazione vale sia per edifici di nuova progettazione che l’adeguamento di edifici esistenti che risultassero essere a rischio di collasso progressivo. Le linee guida prevedono l’uso della analisi statica lineare per tutte le strutture che possono essere considerate come regolari senza la necessità di calcolare il DCR. Nel caso in cui la struttura risultasse irregolare deve essere calcolato il DCR per ogni sezione e verificare che esso non sia superiore a 2. Nel caso in cui una sola sezione supera il valore di DCR prestabilito, l’analisi statica lineare non può essere usata.

Calcolo del DCR

Per il calcolo del DCR si crea un modello tridimensionale della struttura, si effettua l’analisi statica lineare e si calcolano i valori per ogni singolo elemento:

DCR = Q_UDLim/Q_CE

dove:

• Q_CE è la resistenza dell’elemento
• Q_UDLim è l’azione nell’ elemento dovuta ai carichi

   

Carichi

La struttura deve essere verificata in due condizioni di carico differenti:

• Analisi e verifiche in termini di deformazioni;
• Analisi e verifiche in termini di forze.

Nel caso delle analisi con verifiche in termini di deformazioni, le condizioni di carico sono:

Per le aree vicino l’elemento di supporto verticale rimosso e quelle al di sopra di esse si ha:

G_LD = Ω_LD [(0.9 o 1.2)∙D+(0.5∙L o 0.2∙S)]

dove:

• G_LD sono carichi gravitazionali incrementati per l’analisi statica lineare a controllo di deformazioni;
• D sono i carichi permanenti;
• L-S sono rispettivamente i carichi variabili o carico da neve;
• Ω_LD fattore di incremento dinamico per l’analisi statica lineare a controllo di deformazioni.

Per le restanti parti della struttura la condizione di carico è la seguente:

G=(0.9 o 1.2)∙D + (0.5∙L o 0.2∙S)

Nel caso di analisi con verifiche in termini di forze le condizioni di carico sono le seguenti:

Le aree vicino l’elemento di supporto verticale rimosso e quelle al di sopra abbiamo:

G_LF = Ω_LF [(0.9 o 1.2)∙D+(0.5∙L o 0.2∙S)]

dove:

• G_LF sono carichi gravitazionali incrementati per l’analisi statica lineare a controllo di forze;
• D sono i carichi permanenti;
• L ed S sono rispettivamente i carichi variabili o carico da neve;
• Ω_LF fattore di incremento dinamico per l’analisi statica lineare a controllo di forze.

Per le restanti parti della struttura la condizione di carico è la stessa utilizzata in precedenza:

Per mettere in conto la stabilità nei confronti dei carichi laterali e gli effetti PΔ in entrambi i casi si applica ad ogni facciata dell’edificio, per ogni direzione principale (una per volta), la seguente quantità:

L_LAT=0.002∙∑P

dove:

• L_LAT carichi laterali per effetto PΔ;
• ∑P Somma dei carichi verticali (Peso proprio, permanenti e variabili) agenti ad ogni piano, al netto del DIF fattore di incremento dinamico.

Fattore di incremento del carico Ω

Il fattore di incremento dinamico del carico è fornito dalle linee guida in tabella 1:

   

dove

m_LIF è il minore degli m dell’intera struttura, ed i valori di m sono calcolati attraverso la tabella 2.

Verifica

Per il sistema a controllo di spostamenti si deve verificare che:

Φ∙m∙Q_CE ≥ Q_UD

dove:

• Q_UD è l’azione derivante dall’analisi statica lineare;
• m è il fattore modificatore dell’elemento calcolato come specificato nelle linee guida;
• Φ è il fattore di riduzione della resistenza del materiale;
• Q_CE è la resistenza dell’elemento strutturale.

Per il sistema a controllo di forze si deve verificare che:

Φ∙Q_CL ≥ Q_UF

dove:

• Q_UF è l’azione derivante dall’analisi statica lineare;
• Q_CL è la resistenza dell’elemento strutturale;
• Φ è il fattore di riduzione della resistenza del materiale.  

   

   

Analisi statica non lineare Push-down (ASNL)

L’analisi statica non lineare in questo caso denominata push-down ci permette di seguire il comportamento della struttura a seguito di azioni che ne provocano il superamento della soglia elastica fino al collasso.

Il vantaggio di questa procedura è la sua capacità di evidenziare gli effetti non lineari di tipo meccanico e geometrico, determinandone i limiti elastici e di rottura della struttura oppure come condizione iniziale per l’esecuzione di analisi dinamiche non lineari e la validazione dei risultati ottenuti da quest’ultima.

Tramite le analisi statiche non lineari è possibile portare in conto e valutare:

• Le ridistribuzioni dei carichi dovuti a uno o più fallimenti di elementi strutturali primari e/o secondari tramite l’Alternate Path method;
• La formazione progressiva di cerniere plastiche e lo sfruttamento in duttilità di rotazione fino al valore ultimo;
• Le modalità di collasso fragile: quali la rottura a taglio, dei nodi, lo sfilamento delle barre e il buckling delle armature longitudinali compresse;
• L’effetto delle tamponature tramite la riduzione del carico di collasso per formazione di meccanismi resistenti a puntone compresso;
• L’effetto dei grandi spostamenti in elementi trave e solai che conferiscono alla struttura resistenze extra dovute ai meccanismi di tipo catenaria e di membrana.

Le analisi pushdown, di una struttura danneggiata, possono essere eseguite in due differenti modi a seconda di come si applicano le azioni sulla struttura:

1. pushdown uniforme con incremento dei carichi su tutta la struttura;
2. pushdown uniforme con incremento di carico su campata soggetta a danneggiamento.

Nella push-down uniforme (figura 7) si aumentano i carichi gravitazionali incrementali proporzionalmente fino a raggiungimento della massima capacità portante.

L'errore può verificarsi al di fuori delle zone non interessate direttamente dal danneggiamento e quindi non è sempre possibile stimare la capacità residua della struttura danneggiata.

Nell'analisi pushdown per campata (figura 8), il carico gravitazionale viene aumentato proporzionalmente solo nelle campate che hanno subito danni (zone di fallimento degli elementi strutturali) fino al raggiungimento della massima capacità portante.   

   

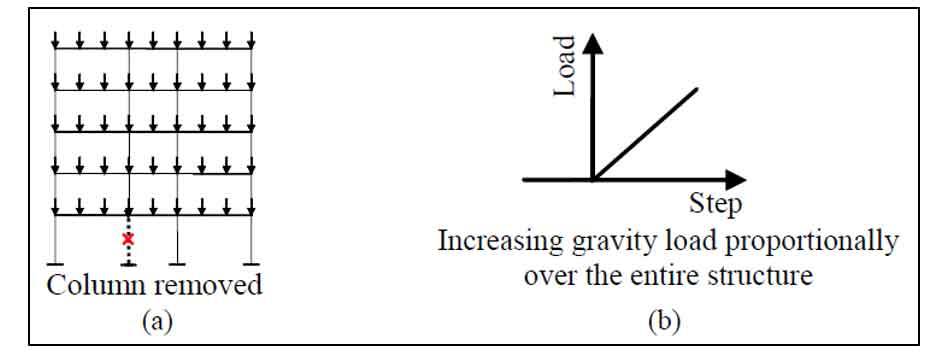
Con tale approccio di caricamento della struttura è possibile stimare la capacità residua come rapporto tra il valore finale del carico ultimo e quello applicato riferito alla parte danneggiata.

    

Le analisi push-down a controllo di forza non vengono condotte in quanto gli effetti geometrici non lineari e quelli meccanici fanno in modo che la struttura presenti una curva di capacità con punti limite locali, tratti di softening e hardening geometrico dovuto ad effetti catenary action, per cui normalmente si procede in questi casi con metodi a controllo di spostamento o arc-length.

Lo schema di caricamento dell'analisi pushdown che considera gli effetti della perdita istantanea della colonna (soggetta a fallimento) è mostrato nella figura 9:

• step 1: applicazione del carico di base (DL + 0,25LL) alla struttura;
• step 2: rimozione della colonna soggetta a fallimento strutturale. In primo luogo, tutte le forze nell’elemento vengono ottenute dal modello strutturale sottoposto al carico applicato, quindi, la struttura viene rimodellata senza una colonna con le sue forze (P, V e M) applicate alla stessa come reazioni per mantenere la posizione di equilibrio. Infine, le stesse forze vengono riapplicate in direzione opposta al fine di annullare il contributo della colonna rimossa;

•  Step 3: applicare il carico aggiuntivo (DL + 0,25LL) al di sopra delle campate contigue a quella della colonna rimossa dove si innesca il danneggiamento fino al completo caricamento o divergenza dell’analisi. Dal momento che non è noto se il carico 2 (DL + 0,25LL) può essere applicato o meno alla struttura, viene introdotto il fattore α per rappresentare la combinazione di carico α (DL + 0,25LL) che la struttura può sopportare. L'instabilità della struttura nella procedura di analisi (ovvero la divergenza del programma) è definita come criterio di controllo.

    

Carichi e combinazioni di carico

L’analisi viene effettuata secondo le stesse combinazioni di carico utilizzate per il metodo statico lineare, ossia, carichi verticali incrementati per le aree di piano al di sopra delle colonne rimosse o delle pareti, tramite un fattore di incremento dinamico Ω_N leggermente diverso rispetto al caso lineare.

   

L'ARTICOLO PROSEGUE NELL'ALLEGATO DOVE E' PRESENTE LA VERSIONE COMPLETA IN FORMATO PDF SALVABILE E STAMPABILE