Identificazione dinamica, aggiornamento del modello e posizionamento ottimale dei sensori per un ponte in calcestruzzo precompresso

Attraverso la Frequency Domain Decomposition (FDD), sono state stimate le frequenze e le forme modali della struttura

L'analisi delle vibrazioni strutturali indotte da azioni naturali o artificiali consente la valutazione di frequenze, forme modali e smorzamenti di una struttura (Rainieri et al 2014, Ren et al 2014), ovvero di effettuare la cosiddetta identificazione dinamica. Nel caso in cui tale identificazione sfrutti l’eccitazione prodotta dall’ambiente circostante, si parla di analisi modale operazionale (OMA).

I risultati di un processo di identificazione, ovvero le proprietà modali della struttura, possono essere adottate per la calibrazione del modello numerico della stessa al fine di ridurre le incertezze di modellazione.
In questo contributo è descritto l’aggiornamento del modello numerico di un viadotto ferroviario in cemento armato precompresso (c.a.p.) a cavi scorrevoli a partire dai risultati di identificazione dinamica eseguita tramite la tecnica della Frequency Domain Decomposition (FDD), che permette la stima delle frequenze e delle forme modali della struttura in esame.

Inoltre, il modello numerico rifinito sulla base di una prima serie di acquisizioni è utilizzato per la definizione di una configurazione di accelerometri (indicati nel seguito anche come sensori) da utilizzarsi per ripetere l’identificazione dinamica della struttura in momenti successivi. A tal fine, si è utilizzata una tecnica di Optimal Sensor Placement (OSP) nota come Effective Indipendence Method (EfI) (Kammer 1991), la quale permette di definire una graduatoria di importanza dei sensori in funzione della loro posizione.

Poiché l’EfI definisce la graduatoria ma non un criterio di selezione del numero ottimale di sensori, si è utilizzata anche la metodologia proposta in (Testa G. et al 2021) che, come descritto nel seguito, fornisce una configurazione ottimale in funzione della differenza tra le frequenze naturali della struttura ottenute mediante analisi modale su modello numerico e quelle ottenute mediante FDD applicata a storie di accelerazione simulate con lo stesso modello numerico.

Frequency Domain Decomposition

Il FDD è un metodo output-only utile a identificare le frequenze di vibrazione e le corrispondenti forme modali di un sistema strutturale partendo dalle accelerazioni registrate sulla struttura (output); si basa sull’asserzione che gli autovettori, che rappresentano i modi di vibrare, costituiscono una base, essendo linearmente indipendenti, per cui qualsiasi spostamento del sistema può essere rappresentato da una loro combinazione lineare ed è possibile disaccoppiare le componenti dei vari modi. Quest’ultima proprietà può essere applicata alla risposta del sistema, misurata in ciascun punto in cui è posizionato l’accelerometro, oppure alla densità spettrale (Power Spectral Density, PSD) della storia accelerometrica, tramite una scomposizione ai valori singolari (Singular Value Decomposition, SVD) della matrice che la rappresenta ad ogni frequenza ω (Wall et al., 2003).

Le frequenze e forme modali forniti da questa procedura sono maggiormente validi quanto più sono verificate le seguenti condizioni: (i) l’eccitazione è un rumore bianco gaussiano a media nulla e deviazione standard unitaria; (ii) le forme modali individuate sono ortogonali; (iii) la struttura ha un coefficiente di smorzamento basso (Brinker et al 2000).

Inoltre, è da tenere presente che al numero di accelerometri utilizzati, S, corrispondono altrettanti gradi di libertà rappresentativi per la struttura.
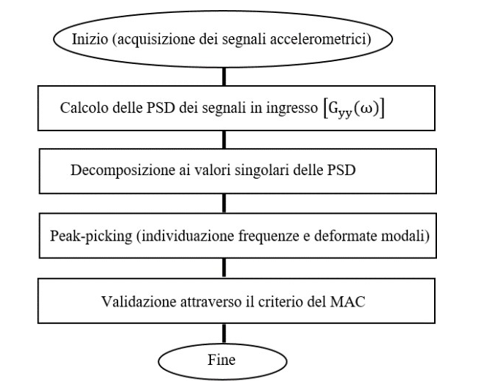
Nel processo di identificazione FDD, riassunto schematicamente nel diagramma di flusso di Figura 1, il primo passo da seguire consiste nella stima delle PSD ricavate attraverso le trasformate di Fourier dei segnali. In particolare, al variare della frequenza ω, nel range di interesse per la struttura in esame e compatibile con le frequenze di campionamento dei segnali registrati dagli accelerometri, si individuano le matrici PSD di ordine S.

Come secondo passo, la matrice in cui sono allocate le PSD dei segnali in ingresso, indicata come [G_yy(ω)], è scomposta considerando la SVD come riportato nell’eq. (1) dove l’apice H denota che la matrice è hermitiana:

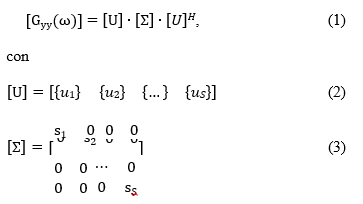
Per ogni frequenza si hanno tre matrici, di cui una diagonale [Σ] contenente i valori singolari (s1, s2, …, sS), il primo dei quali rappresenta l’intensità del modo predominante, mentre gli altri rappresentano l’intensità del rumore o dei modi vicini a quello dominante. I valori singolari sono dunque le densità spettrali dei sistemi ad un grado di libertà ed infatti sono tanti quanti gli accelerometri utilizzati per la struttura in esame e quindi rappresentativi dei gradi di libertà del sistema strutturale. Le altre due matrici [U] contengono i vettori singolari ({𝑢1}, {𝑢2}, … , {𝑢𝑆}) che portano con sé le informazioni delle relative forme modali.

Il terzo passo consiste nella rappresentazione grafica dello spettro dei valori singolari da cui è possibile riconoscere i picchi che rappresentano i modi da identificare. Infatti, le frequenze naturali associate ad un modo si identificano graficamente mediante la tecnica del peak-picking. A ciascun picco individuato è associato un valore singolare a cui corrispondono i vettori singolari. Si ritiene che il primo vettore singolare ben approssimi gli spostamenti modali della struttura nei punti in cui sono state eseguite le letture in accelerazione.

Il metodo FDD consente anche di identificare possibili modi accoppiati, che non sono distinguibili con altri metodi, quando ad una frequenza più di un vettore singolare presenta un valore di picco.
L’ultimo passo, che consente di interpretare correttamente, e quindi di verificare i risultati ottenuti, è il confronto di questi ultimi.

Il confronto può essere eseguito tra i risultati ottenuti dall’analisi sperimentale oppure tra i risultati dell’analisi sperimentale e quelli dell’analisi numerica (modello FEM). Nel primo caso si valuta il grado di somiglianza tra i modi individuati mentre nel secondo caso si valutare il grado di rispondenza tra il comportamento reale della struttura (valutato con l’analisi sperimentale) e quello ipotizzato in fase di progetto (valutato con l’analisi numerica).

L'ARTICOLO CONTINUA NEL PDF IN ALLEGATO...

La presente memoria è tratta da Italian Concrete Conference - Napoli, 12-15 ottobre 2022
Evento organizzato da aicap e CTE