La verifica sperimentale dei modelli di pericolosità sismica
I modelli di pericolosità devono essere verificati sperimentalmente con i dati disponibili. Tuttavia, la loro “accettazione” per la normativa necessita anche di una discussione sul “come” vengono utilizzati. La normativa in Italia non considera le incertezze ed è quindi soggetta a grandi variazioni anche per stime non statisticamente differenti.
La pericolosità sismica come modello scientifico
Le analisi di pericolosità sismica hanno lo scopo di prevedere probabilisticamente gli scuotimenti del terreno dovuti ai futuri terremoti in un certo intervallo spazio-temporale. La natura probabilistica di queste stime è a tutt’oggi inevitabile e deriva dall’impossibilità di prevedere con certezza i prossimi terremoti e gli scuotimenti massimi del terreno che ne deriveranno.
Le complessità intrinseche dei meccanismi di sorgente dei terremoti e della propagazione delle onde sismiche in prossimità dell’epicentro rendono impossibili anche stime realistiche degli scuotimenti massimi attesi in un’area, come peraltro suffragato dalle evidenze di molti terremoti in tutto il mondo. Di conseguenza, un modello di pericolosità sismica realistico deve includere tutto ciò che i sismologi conoscono sull’accadimento dei terremoti e sulla propagazione delle onde sismiche, e, necessariamente, anche tutte le incertezze conosciute su tali processi. Queste incertezze vengono di solito rappresentate (vedi Figura 1) con un insieme di distribuzioni, o curve di pericolosità, ognuna delle quali è ottenuta da un modello diverso, oppure con diverse parametrizzazioni dello stesso modello.
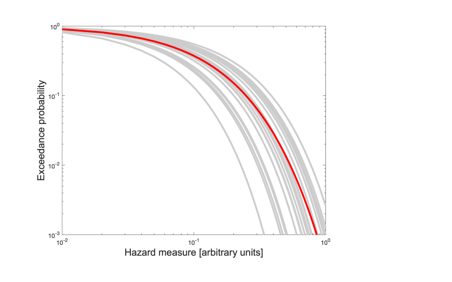
L’insieme delle curve deriva da diversi modelli, oppure dalla diversa parametrizzazione di un unico modello (rami di un albero logico). In sintesi, nessuno conosce il modello “vero”, ma si assume che, se il modello è corretto, l’insieme di curve definisca l’incertezza epistemica, ovvero dove la curva del vero modello possa essere.
Nella normativa per costruzioni in zona sismica in Italia questo tipo di incertezza non viene considerata ma si utilizza una unica curva di pericolosità, che può essere solitamente la media (curva in rosso), o la mediana (come nel modello di pericolosità attualmente in uso per la normativa ). Di fatto, non si distingue il caso in cui l’insieme di curve sia molto vicino (bassa incertezza epistemica) o molto disperso (alta incertezza epistemica) intorno alla curva considerata nella normativa.
L’implicita natura puramente scientifica delle analisi di pericolosità sismica (che, in sintesi, stima cosa farà la natura nel futuro prossimo) suggerirebbe che la valutazione di tali modelli debba seguire i metodi canonici usati in tutte le altre discipline fisiche. Questa attitudine è di fatto perseguita per la verifica dei modelli più recenti sviluppati in Italia (MPS19 ) e nel resto del mondo.
Tuttavia, la natura probabilistica di tali stime, le incertezze di diversa natura, e il numero limitato di osservazioni di scuotimento del terreno rende questa fase di test tutt’altro che agevole. In particolare, la verifica sperimentale di modelli probabilistici richiede una discussione approfondita e non banale sul “se” e sul “come” le stime di un modello probabilistico possano essere verificate scientificamente.
Per esempio, la celeberrima e comune citazione – “tutti i modelli sono sbagliati (anche se qualcuno può essere utile)” – sembrerebbe porre dubbi sostanziali sulla necessità di verificare sperimentalmente un singolo modello probabilistico: se tutti i modelli sono sbagliati, e lo sappiamo già, ha senso la verifica sperimentale di un modello? Questo è il motivo per cui molti matematici e scienziati ammettono solo il confronto tra previsioni probabilistiche di diversi modelli per verificare quale sia il migliore, senza però fornire una valutazione assoluta sulla “bontà” statistica di nessuno di questi modelli.
In questo articolo non affronteremo questo punto di estrema importanza che è stato ampiamente discusso in molti articoli, ma assumeremo che tale verifica sperimentale sia possibile e abbia senso. In questa visione, la verifica sperimentale prende il nome di test di consistenza del modello se nella fase di test si usano dati in qualche modo usati per la costruzione del modello stesso, e validazione nel caso in cui i dati siano totalmente indipendenti dalla costruzione del modello.
Sebbene la validazione possa richiedere tempi anche molto lunghi per modelli che fanno previsioni su un intervallo temporale di decadi, come i modelli di pericolosità sismica per la normativa per costruzioni in zona sismica in Italia (chiamata in questo articolo “normativa” per brevità), i test di consistenza sono certamente possibili anche se il numero limitato di dati di scuotimento del terreno a disposizione rendono questi test poco “potenti” in termini statistici; in altre parole, molti modelli, anche diversi tra loro, possono risultare compatibili con le poche osservazioni a disposizione.
A tale proposito è sempre utile rimarcare che, contrariamente a quanto spesso impropriamente sostenuto, la credibilità di un modello probabilistico non può essere verificata a posteriori con le osservazioni di un singolo terremoto.
I modelli di pericolosità sismica non vengono valutati solamente utilizzando il numero limitato di dati degli scuotimenti del terreno (in particolare per terremoti di interesse per la pericolosità sismica orientata alla normativa), ma vengono anche valutati “a pezzi”; per esempio i test di consistenza vengono effettuati anche per i modelli di accadimento dei terremoti, che rappresentano solo una parte dei modelli di pericolosità.
L’idea di base è che se il modello di accadimento dei terremoti non è consistente con il numero e la localizzazione dei terremoti del catalogo storico e strumentale, anche il modello di pericolosità nel suo insieme non può essere ritenuto credibile. Si noti però che non è vero il contrario, cioè se il modello di accadimento dei terremoti è consistente con il catalogo storico dei terremoti, non possiamo dire nulla sulla realisticità del modello di pericolosità che include anche altri ingredienti, come la modellazione della propagazione delle onde sismiche nel terreno.
A scopo di esempio, riportiamo in Figura 2 un risultato della fase di test di consistenza per il modello di sismicità medio utilizzato nella preparazione di MPS19.
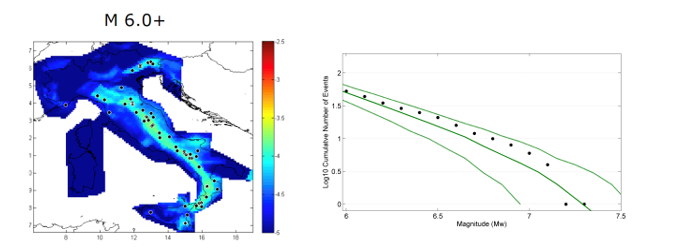
Un altro modo di verifica della consistenza del modello di pericolosità si basa sul confronto tra le previsioni probabilistiche del modello e le osservazioni delle intensità macrosismiche osservate in siti dove la qualità dei dati sia sufficientemente buona per tale confronto.
Tale tipo di test di consistenza ha diversi aspetti critici che vanno presi in considerazione; per esempio: (i) le consistenti incertezze nel passaggio da intensità macrosismica a valori numerici degli scuotimenti come accelerazioni e velocità, e viceversa; (ii) le incertezze sulle intensità macrosismiche del passato sono affette da incertezze a volte sostanziose e sostanziali dovute, per esempio, all’effetto cumulato di terremoti di una sequenza sismica e alla tipologia di suolo che non è considerato nel modello di pericolosità (per definizione, il modello di pericolosità per la normativa si riferisce ad un suolo rigido); (iii) le stime di intensità macrosismica a volte dipendono dal gruppo di ricerca che le stima. Oltre a queste criticità, esistono altri modi in cui le incertezze sulle intensità macrosismiche possono influenzare in maniera indiretta i test di consistenza del modello, poiché le magnitudo dei terremoti storici sono ottenuti dalle intensità macrosismiche. Questo ultimo aspetto non verrà considerato oltre in questo articolo.
Un aspetto spesso trascurato nella fase di valutazione scientifica di un modello di pericolosità sismica è che tradizionalmente tale modello si basa sugli scuotimenti provocati dai cosiddetti mainshock, cioè i terremoti più grandi di una sequenza, assumendo che per la normativa questi eventi siano i più importanti per la salvaguardia della vita umana. Di conseguenza, la verifica scientifica di questi modelli di pericolosità dovrebbe utilizzare solo gli scuotimenti del terreno generati da tali terremoti. Ciò però implica la rimozione di scuotimenti forti del terreno osservati in alcuni siti, perché generati da cosiddetti foreshock o aftershock, cioè terremoti forti che anticipano o seguono i mainshock in finestre temporali e spaziali molto piccole. Sebbene questa esclusione nella fase di verifica sia una necessità per paragonare “mele” con “mele”, potrebbe apparire poco ragionevole rimuovere gli scuotimenti dei terreni che in alcuni siti hanno generato scuotimenti anche più forti del mainshock stesso. Per superare questo impasse, i sismologi hanno iniziato a preparare modelli di pericolosità che tengano conto di tutti i terremoti aspettati e non solo dei mainshock. In Figura 3 riportiamo le differenze tra un modello di pericolosità classico (solo con mainshock) ed uno che tenga conto delle sequenze sismiche sviluppato nell’ambito del modello di pericolosità MPS19. Si noti che per periodi di ritorno di 475 anni (corrispondenti a valori di scuotimento che hanno il 10% di probabilità di essere superati in 50 anni) le variazioni della PGA per tali tempi di ritorno in aree di alta sismicità possono essere anche superiori al 20%.
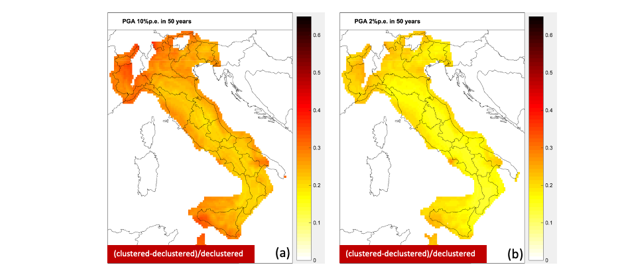
L'ARTICOLO CONTINUA NEL PDF IN ALLEGATO...
Controlli
Una raccolta di approfondimenti per chi si occupa di fare controlli e verifiche dei materiali nel settore delle costruzioni e dell'edilizia.

Ingegneria Strutturale
Tutto quello che riguarda il tema dell’ingegneria strutturale: innovazione digitale, modellazione e progettazione, tecniche di costruzione e di intervento, controlli e monitoraggi, soluzioni per il miglioramento, evoluzione normativa, approfondimento di casi concreti e pareri degli esperti.
Sicurezza
Gli approfondimenti e le news riguardanti il tema della sicurezza intesa sia come strutturale, antincendio, sul lavoro, ambientale, informatica, ecc.

Sismica
Tutti gli articoli pubblicati da Ingenio nell’ambito della sismologia e dell’ingegneria sismica.
Condividi su: Facebook LinkedIn Twitter WhatsApp
