Valutazione del comportamento sismico dei ponti ad arco in muratura

L’arco in muratura

Lo studio degli archi murari resta un tema sempre attuale, grazie alla notevole diffusione di tale tipologia. Numerosi sono i ponti antichi giunti fino ai nostri giorni, ma altrettanto numerosi sono quelli realizzati nel secolo scorso, specie in campo ferroviario. Per i primi, nei quali prevale l’interesse storico ed artistico, si pone il problema del recupero e del rafforzamento nel rispetto delle loro caratteristiche architettoniche, anche accettando eventuali limitazioni d’uso; per i secondi va valutata l’adeguatezza a sopportare i nuovi carichi stradali o ferroviari.

Nella storia delle costruzioni l'arco ha rappresentato certamente una delle invenzioni più importanti, costituendo l’unica possibilità per superare grandi luci con materiali non resistenti a trazione, ed è stata la più diffusa tipologia nella costruzione dei ponti, fino alla metà dello scorso secolo.

Nonostante il diffuso utilizzo già nelle antiche civiltà (l’arco era conosciuto in Egitto, a Babilonia, in Persia e nella Magna Grecia) e il largo impiego da parte dei Romani, fino al XVII secolo gli archi erano progettati senza conoscerne il reale comportamento statico. Leonardo da Vinci aveva capito l'importanza della spinta ma non riuscì a fornire regole di progettazione efficaci. Va ricordato il suo progetto di ponte ad arco di 240 m di luce (freccia = 57 m, spessore variabile da 42 m, alle imposte, a 9 m, in chiave) per superare il Corno d'Oro a Istanbul, non realizzato per le ovvie difficoltà esecutive, ma staticamente valido.

Nella pratica ci si affidava a regole empiriche, che stabilivano gli spessori in chiave e alle imposte in funzione della luce o del raggio di curvatura e le dimensioni delle pile, facendo affidamento sulle realizzazioni precedenti. Finalmente, nel 1676, Hooke suggerì che la forma ottimale di un arco è quella che si ottiene e ribaltando quella che una fune assume sotto il peso proprio: “Ut pendet continuum flexile, sic stabit continuum rigidum inversum”. Nel 1697, Gregory ricavò l'equazione della catenaria. Nel suo primo "Traité des Ponts", del 1714, Gautier suggeriva regole empiriche per il progetto, parlava della spinta ma non forniva regole di calcolo.

Nel XVIII secolo il calcolo a rottura degli archi ebbe un enorme sviluppo, grazie ai contributi di eminenti studiosi, tra cui Coulomb e Mascheroni, e alla fine del '700 la statica degli archi era nota: l'equilibrio dell'arco è un problema geometrico piuttosto che un problema di resistenza dei materiali e, di conseguenza, il collasso è collegato essenzialmente alla forma. I modelli facevano riferimento alle condizioni di rottura e all'individuazione del relativo meccanismo. Gli studi successivi, come quelli di Lamé e Clapeyron (1823) e quelli sperimentali di Boistard (1800), sembravano confermare i risultati teorici precedentemente ottenuti.

Nell'800, la diffusione della teoria dell'elasticità determinò un cambiamento di rotta. Navier, nel 1826, introdusse l'ipotesi di distribuzione lineare delle tensioni nella sezione pressoinflessa, suggerendo la regola del terzo medio per le sezioni rettangolari. Méry, nel 1840, propose la ben nota tecnica di verifica dell'arco, in presenza di un assegnato carico, con la costruzione di una funicolare passante per tre punti, uno al terzo medio superiore in chiave e gli altri due al terzo medio inferiore in prossimità delle imposte: l'arco è totalmente reagente se la funicolare si conserva ovunque all'interno dei terzi medi. La questione della ricerca della effettiva curva funicolare del carico fu affrontata da Rankine (1862) e poi di Hagen e Winkler (1879), che proposero di individuare la funicolare minimizzando la somma dei quadrati delle sue distanze dall'asse, e da Castigliano (1879) che, invece, propose il metodo della minima energia di deformazione; ben nota è la sua analisi del Ponte Mosca di Torino.

Raccogliendo anche ulteriori studi della prima metà del ‘900, negli anni ’60 del secolo scorso, Heyman particolarizzò alle strutture murarie l'analisi limite, nel frattempo sviluppata per le strutture metalliche, proponendo il modello di arco a conci lapidei indeformabili, semplicemente accostati a secco, e formulando tre ipotesi sulle sezioni di interfaccia tra i conci:

• attrito molto elevato da scongiurare lo scorrimento tra i conci;
• resistenza a trazione nulla;
• resistenza a compressione infinita.

Mentre le prime due ipotesi sono soddisfatte, la terza limita la validità del metodo ai soli archi realizzati con materiale molto resistente.

Nel presente articolo, si presenta il modello di arco a conci lapidei di materiale con resistenza a compressione finita. Una procedura iterativa consente di individuare il meccanismo di rottura e il corrispondente moltiplicatore del carico variabile agente. Si introduce dapprima il modello con riferimento al comportamento in presenza di carichi viaggianti, successivamente ci si sofferma sul comportamento in presenza di azioni sismiche.

Analisi limite di un arco in muratura

Dominio limite della sezione rettangolare

Sia la muratura caratterizzata da resistenza a trazione nulla e un comportamento rigido – perfettamente plastico a compressione, con resistenza a rottura pari a 𝑓_𝑢.

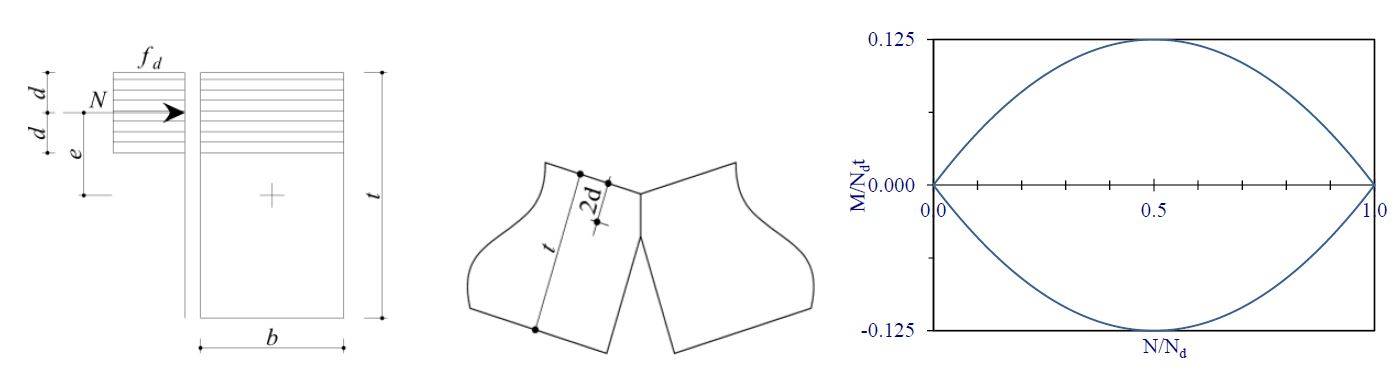
La resistenza di calcolo è 𝑓_𝑑=𝑓_𝑢/γ_M, essendo γ_M il fattore parziale della muratura. Pertanto, in una sezione, di larghezza b e altezza t, al collasso in presenza di uno sforzo normale N agente ad una distanza d dall’estremità, il diagramma delle tensioni è uniforme su un tratto 2d dall’estremità (Figura 1).

Il dominio limite nel piano (N, M) è formato da due archi di parabola simmetrici rispetto all’asse N: M=±(bt²)⁄2∙𝑓_𝑑 N⁄N_d ∙(1-N/N_d ), essendo N_d=bt𝑓_𝑑 lo sforzo normale di completa plasticizzazione della sezione. Le coppie (M, N) del dominio corrispondono a stati limite in cui le due sezioni adiacenti possono ruotare l’una rispetto all’altra intorno al punto di inizio del diagramma delle tensioni, formando una cerniera (Figura 1).

Si nota che, nell’ipotesi di resistenza a compressione infinita (𝑓_𝑑→∞), i due archi di parabola degenerano nelle due rette M=±N∙t⁄2, tangenti alle parabole nell’origine, e la risultante delle azioni cade all’estradosso o all’intradosso della sezione, che rappresenta anche il centro di rotazione relativo delle due sezioni.

Il collasso dell'arco

L’arco è sul punto di collasso quando, al crescere del carico variabile, si formano almeno quattro cerniere che lo trasformano in un meccanismo. Per l’ipotesi sul materiale, tutte le cerniere si formano contemporaneamente. Il teorema di unicità assicura che la soluzione esiste ed è unica e tale è il moltiplicatore di rottura del carico. L’arco è, invece, in sicurezza sotto un assegnato carico se esiste una soluzione, ossia una funicolare del carico, per la quale i punti individuati dalle coppie (M, N) sono sempre all’interno del dominio limite.

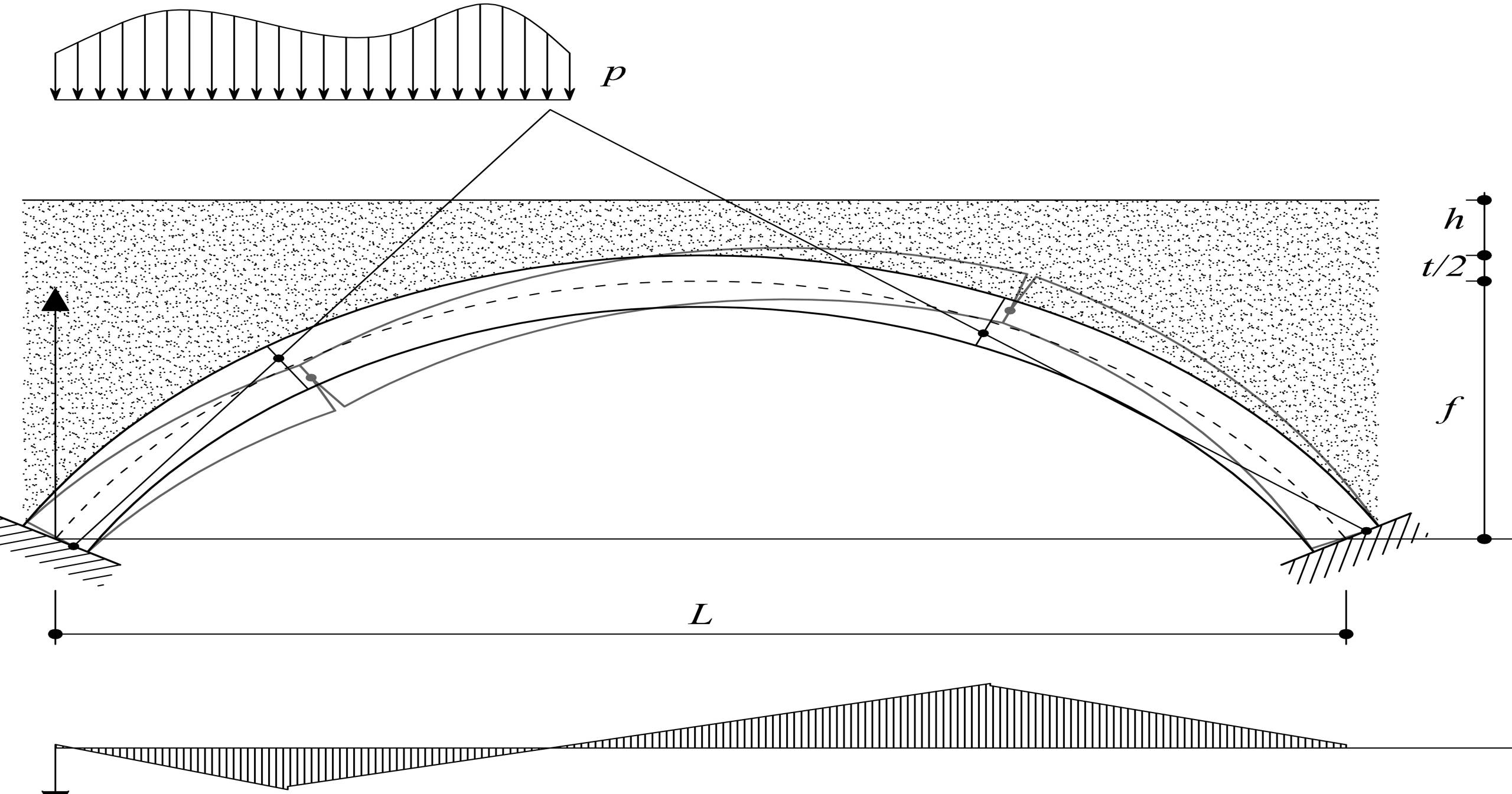
Si consideri un arco di luce L, freccia 𝑓, spessore t (per semplicità costante) e altezza del ricoprimento h (Figura 2).

Il carico permanente w è dato dalla somma del peso proprio dell’arco stesso w_w e di quello del rinfianco/riempimento w_b, entrambi variabili lungo l’asse longitudinale z. Si consideri anche un carico verticale mobile p, in generale variabile lungo l’asse longitudinale z (per esempio, a tratti).

Si supponga che esiste una soluzione sotto i soli carichi permanenti nella quale i punti rappresentanti gli stati di sollecitazione nel piano (M, N) sono sempre all’interno del dominio limite della sezione.

Come ben noto, il moltiplicatore di collasso è il massimo dei moltiplicatori staticamente ammissibili (moltiplicatore per il quale l’arco è in sicurezza) e il minimo dei moltiplicatori cinematicamente sufficienti (moltiplicatore per il quale l’arco si trasforma in un meccanismo). Pertanto, meccanismo di collasso e corrispondente moltiplicatore del carico possono essere ricercati con un procedimento iterativo che va avviato assegnando un meccanismo di primo tentativo, fissando le posizioni delle cerniere, ossia sezioni e distanza della risultante dal bordo compresso.

L’equazione di equilibrio, utilizzando il principio dei lavori virtuali, si scrive:

λ_p L_p+λ_w L_w +λ_b L_b=L_i

dove λ_p, λ_w e λ_b sono i moltiplicatori dei carichi già definiti, L_p, L_w e L_b i rispettivi lavori virtuali e L_i il lavoro interno in corrispondenza delle cerniere. Usualmente alcuni moltiplicatori sono fissati (quelli dei carichi permanenti nella verifica in presenza dei carichi mobili) o sono nulli (quello dei carichi mobili, nella verifica in presenze dei soli carichi permanenti); pertanto, l’incognita è soltanto una e l’equazione fornisce il valore del moltiplicatore cinematicamente sufficiente e, quindi, dei carichi che portano l’arco al collasso. Noti i carichi agenti al collasso, è possibile calcolare le reazioni vincolari esterne e le caratteristiche della sollecitazione in ogni sezione, ossia la funicolare del carico passante per le quattro cerniere assegnate. Il moltiplicatore trovato è anche staticamente ammissibile e, quindi, è il moltiplicatore di rottura se la relativa curva funicolare rispetta in tutte le sezioni la relazione |M|≤(bt²)⁄2∙𝑓_𝑑 N⁄N_d ∙(1-N/N_d ), con l’uguaglianza in un numero di sezioni sufficiente a trasformare l’arco in un meccanismo.

In caso contrario, il procedimento va iterato spostando le cerniere opportunamente nelle sezioni di massimo scostamento e assegnando un’opportuna eccentricità a N.

Nel seguito si valuta dapprima il grado di sicurezza sotto i soli carichi permanenti (λ_p=0), poi si passerà alla verifica sotto i carichi mobili (λ_w=cost,λ_b=cost).

Verifica in presenza dei soli carichi permanenti

Si supponga che esista una funicolare dei soli carichi permanenti, tutta compresa nella sagoma dell’arco e tale che i punti che rappresentano gli stati di sollecitazione in ciascuna sezione siano tutti compresi all’interno del dominio limite: |M|≤(bt²)⁄2∙f_d N⁄N_d ∙(1-N/N_d ).

Il caso di asse dell’arco coincidente con una possibile funicolare del carico permanente (M=0) è un caso particolare, per il quale la precedente condizione degenera in: N≤N_d.
Meccanismo di collasso e relativo moltiplicatore del carico possono trovarsi con la già menzionata procedura iterativa, utilizzando la relazione di equilibrio che si semplifica nella:

λ_w L_w +λ_b L_b=L_i

dove il rapporto λ_b⁄λ_w , è fissato. Va osservato che, nel caso usuale di simmetria strutturale e di carico, il meccanismo deve contenere almeno cinque cerniere (Figura 3).

In alternativa, e più efficacemente, la verifica in presenza dei soli carichi permanenti può essere eseguita individuando lo spessore minimo t_min, definito come quel valore dello spessore per il quale esiste soltanto una funicolare del carico permanente, tutta compresa nella sagoma dell’arco e tale che i punti che rappresentano gli stati di sollecitazione in ciascuna sezione siano tutti compresi all’interno del dominio limite: |M|≤(bt²)⁄2∙f_d N⁄N_d ∙(1-N/N_d ).

Per quanto già detto, l’eguaglianza deve essere verificata in almeno cinque sezioni. Il rapporto tra lo spessore effettivo e quello minimo è una misura del grado di sicurezza in presenza dei carichi permanenti e della capacità dell’arco di sopportare anche carichi mobili.

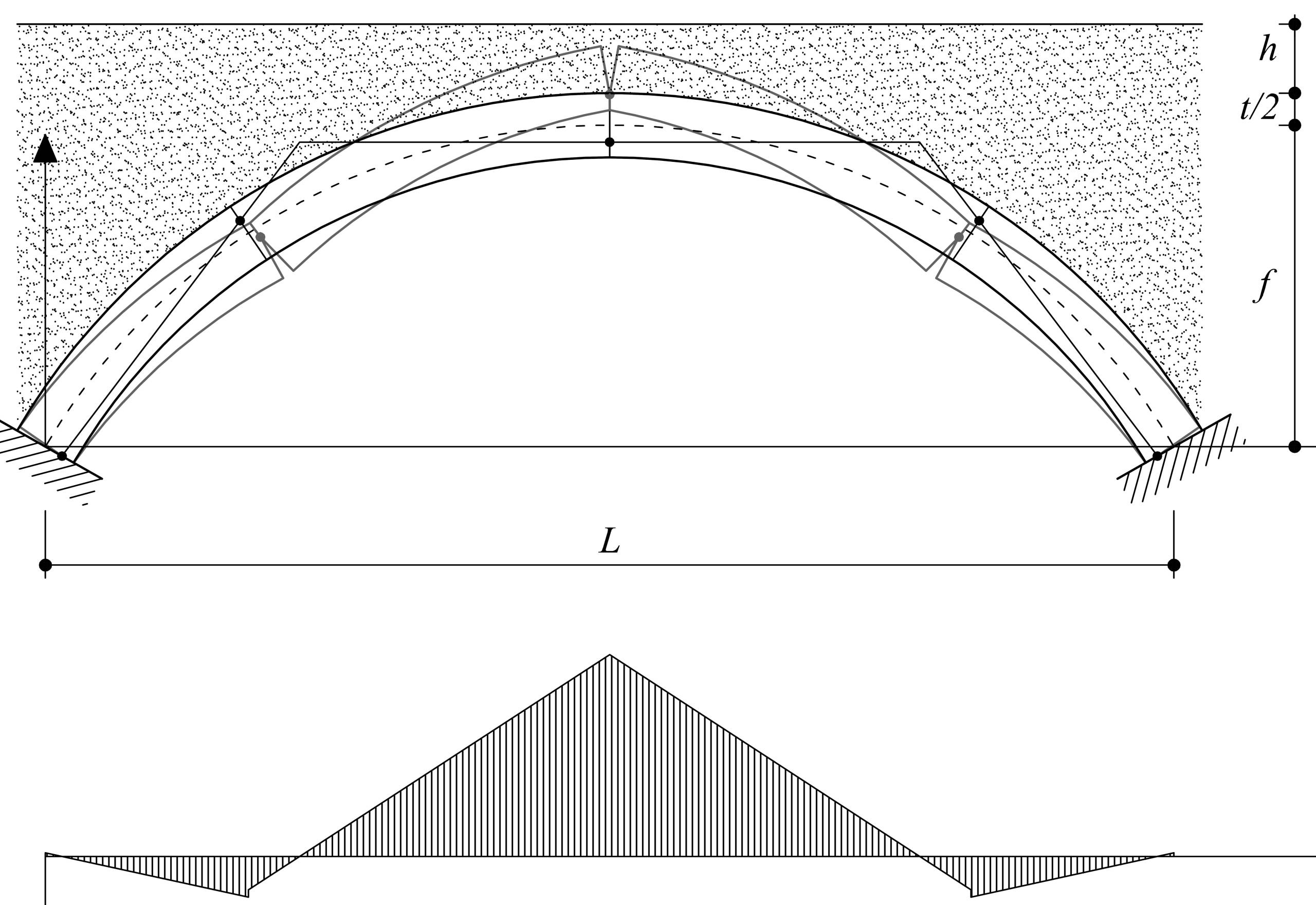
L'articolo continua trattando più nello specifico la verifica con i carichi mobili, legata anche ai parametri geometrici e di carico e analizzando i casi limite in presenza di azioni sismiche

SCARICA* E LEGGI L'ARTICOLO INTEGRALE