Volte in muratura: come considerare la spinta passiva esercitata dal riempimento
Il software Aedes.SAV permette di considerare l'azione della spinta passiva esercitata dal riempimento e di verificare la stabilità delle volte in muratura
I metodi dell'analisi limite, implementati nel software Aedes.SAV, consentono il corretto approccio nei confronti della stabilità delle volte in muratura. Nel modello strutturale vengono studiati l'equilibrio del sistema rigido-fragile ed i meccanismi di collasso dovuti al raggiungimento dei massimi valori consentiti per i carichi applicati.
Carichi non simmetrici possono produrre instabilità teorica della volta: questa configurazione si manifesta tipicamente nei ponti in muratura. L'effettiva capacità della struttura voltata può tuttavia richiedere la modellazione dell'interazione con il riempimento: esso infatti si oppone all'insorgere del cinematismo reagendo con forze orizzontali passive.
Il software Aedes.SAV permette di considerare l'azione della spinta passiva esercitata dal riempimento.
Il giudizio sulla stabilità diviene più realistico, ottenendo un duplice vantaggio:
- si interpreta correttamente il comportamento stabile mostrato da antiche strutture murarie soggette ai carichi moderni (es.: ponti stradali o ferroviari);
- è possibile evitare o ridimensionare interventi invasivi di consolidamento.
L'effetto dei carichi non simmetrici sulle volte in muratura
L'analisi di stabilità delle volte in muratura viene condotta con i metodi dell'analisi limite, implementati nel software Aedes.SAV, studiando l'equilibrio del sistema rigido-fragile ed i meccanismi di collasso dovuti al raggiungimento dei massimi valori consentiti per i carichi applicati. La formazione progressiva delle cerniere, fino ad un numero massimo di 3, e la posizione della curva delle pressioni costituiscono i parametri che caratterizzano il comportamento strutturale delle volte murarie.
E' frequente il caso in cui carichi concentrati posti in posizione non simmetrica rispetto all'asse della volta producono configurazioni di equilibrio al limite di stabilità, se non impossibili. In fig. 1 è rappresentato un esempio di questo tipo.
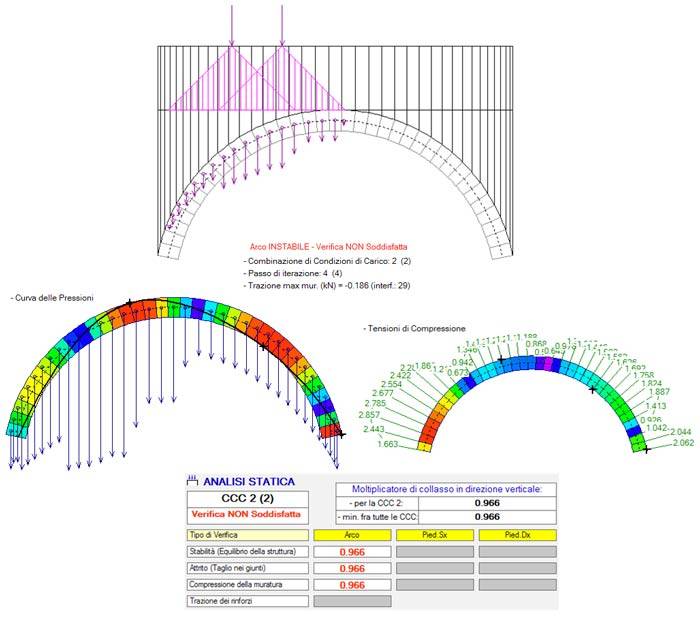
Figura 1
Per carichi concentrati si intendono carichi applicati su un'impronta di limitate dimensioni, per esempio in corrispondenza del piano di viabilità di un ponte in muratura, che subiscono una certa diffusione prima di giungere a sollecitare i conci resistenti dell'arco. Ad una posizione non simmetrica nel piano superiore di viabilità corrisponde una configurazione non simmetrica di azioni verticali sui conci dell'arco.
L'instabilità che può generarsi è descritta dall'impossibilità di determinare una curva delle pressioni interna alla geometria dell'arco anche ammettendo la formazione di tre cerniere alterne, cioè tre punti di contatto fra curva delle pressioni e superfici di intradosso e di estradosso.
Con riferimento al caso rappresentato in fig. 1, uno o più carichi concentrati applicati nella parte sinistra dell'arco possono sollecitare la struttura fino a generare un cinematismo che si muove verso il lato opposto, cioè verso destra.
Il giudizio sfavorevole che viene attribuito alla volta muraria in un caso di questo tipo deve essere valutato con attenzione, ad esempio prendendo in considerazione l'interazione del sistema voltato con le strutture di riempimento, frequentemente trascurata.
Grazie a tale interazione è infatti possibile giustificare la stabilità di una volta muraria sotto l'azione di carichi verticali concentrati asimmetrici che, considerando reagente la sola struttura ad arco, non ammetterebbero una soluzione equilibrata.
Il ruolo del riempimento: la spinta passiva
Il riempimento svolge di per sé un ruolo favorevole nei confronti della stabilità dell'equilibrio della volta: il carico verticale diffuso tende a ricentrare la curva delle pressioni, ossia a diminuirne l'eccentricità rispetto all'asse dell'arco. Oltre a fornire 'peso', ossia carico verticale, si può considerare che il riempimento svolga un ruolo più importante contrastando la deformazione generata dall'attivazione del cinematismo.
Spingendo verso la spalla destra (con riferimento alla fig. 2), la volta trova il contrasto del riempimento: questo corrisponde ad una spinta passiva che il riempimento applica sull'arco, facendo diminuire le eccentricità della curva delle pressioni.
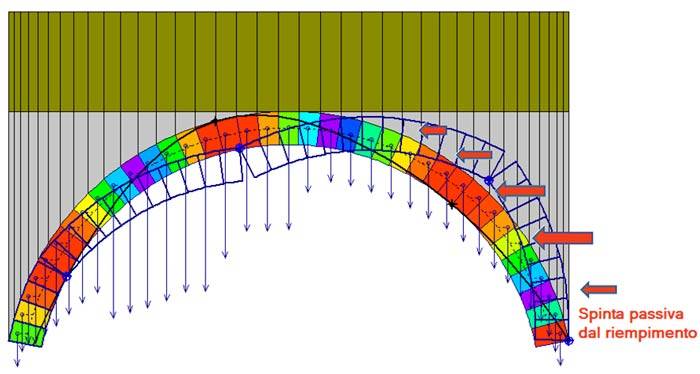
Figura 2
Per modellare la spinta passiva, si ipotizza che la pressione orizzontale dovuta al riempimento sia proporzionale alla pressione verticale del peso proprio esercitata dal materiale di riempimento. La pressione orizzontale alla profondità z (rispetto al piano di viabilità o di calpestio superiore) è quindi pari a:
σ(z) = kp · γ· z
dove il coefficiente di pressione passiva del terreno kp è funzione, nella sua formulazione più generale, dello spostamento dell'arco che spinge sul riempimento. Il valore di kp può tuttavia essere assunto costante, ad esempio contenuto nell'intervallo 0.5-1.0 (nei casi applicativi è possibile determinare il valore di progetto di kp studiando la stabilità dell'equilibrio in funzione della variazione di kp stesso).
Per studiare l'equilibrio dell'arco, le pressioni passive orizzontali vengono tradotte in forze orizzontali (spinte passive S) applicate sui conci che tendono a muoversi verso il riempimento. La forza orizzontale agente su di uno di tali conci è espressa dalla relazione:
S = kp · P · tgα
dove P è il peso della colonna di riempimento che sovrasta il concio stesso.
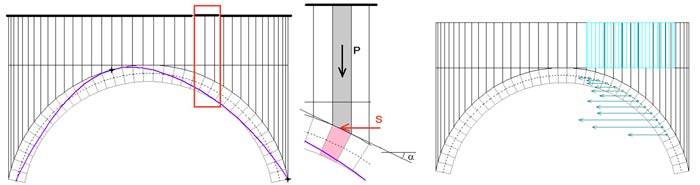
Figura 3
L'azione della spinta passiva determina una curva delle pressioni più centrata, favorendo in tal modo l'equilibrio e la riduzione delle massime tensioni di compressione agenti nelle sezioni dell'arco.
Si deve infine considerare che se la verifica di stabilità dell'arco viene condotta introducendo la spinta passiva, cioè le pressioni passive orizzontali, diventa necessario valutare l'equilibrio delle strutture di sostegno oltre l'arco, ossia delle spalle o delle pareti, sotto l'azione ribaltante delle pressioni che agiscono su tali strutture. Nei ponti queste strutture di sostegno sono massicce e quindi è difficile che tali azioni instabilizzino le spalle.
Come considerare la spinta passiva con il software Aedes.SAV
Il software Aedes.SAV, vers. 2019-2020, permette di considerare l'azione della spinta orizzontale esercitata dal riempimento attraverso la definizione di carichi orizzontali agenti sui conci interessati.
Nel seguito, viene presentato lo studio statico di una volta sottoposta ad un carico non simmetrico rispetto all'asse verticale centrale dell'arco e contemporaneamente alla spinta passiva dovuta al riempimento.
Esempio di una volta sottoposta ad un carico non simmetrico
L'esempio illustrato si riferisce ad un ponte in muratura caratterizzato da un arco circolare quasi a tutto sesto (l'angolo di imposta è 11.3°), di spessore 50 cm.; la profondità della struttura voltata è 240 cm.
L'arco ha una luce interna di 744 cm. e una freccia di 305 cm. Sopra la linea di estradosso di chiave è presente un sottofondo di altezza 150 cm., che insieme al rinfianco costituisce la struttura di riempimento, caratterizzata dal peso specifico di 19 kN/m³.
I carichi agenti sull'arco sono suddivisi nelle seguenti condizioni di carico elementari (CCE):
CCE 1: pesi propri (permanenti g1) della volta muraria, del riempimento (rinfianchi + sottofondo);
CCE 2: una coppia di carichi concentrati Q1k pari a 300 kN (con diffusione a 45° e moltiplicatore verticale selezionato, in modo da valutare il coefficiente di sicurezza nei confronti di tale carico), in posizione non simmetrica, agenti sul semiarco sinistro;
CCE 3: un carico distribuito q1k (anch'esso affetto da moltiplicatore verticale) pari a 21.60 kN/m;
CCE 4: forze orizzontali competenti alla spinta passiva, distribuite sui conci del semiarco destro, cioè sui conci che tendono a spostarsi verso il riempimento destro per effetto del cinematismo indotto dai carichi applicati.
Vengono confrontate le due soluzioni in assenza e in presenza di spinta passiva. Considerando l'effetto delle forze orizzontali passive dovute al riempimento (carichi orizzontali sul semiarco destro in fig. 4) l'arco diviene stabile senza che si formino cerniere e si ha un beneficio significativo anche nei riguardi della massima tensione di compressione. Il miglioramento del comportamento strutturale ottenuto tramite la spinta passiva risulta evidente.
Ne deriva un giudizio definitivo di stabilità soddisfatta e si delinea in tal modo un percorso attraverso il quale è possibile:
- interpretare correttamente il comportamento stabile mostrato da antiche strutture murarie soggette ai moderni carichi, ad esempio nel caso dei ponti stradali o ferroviari;
- evitare o ridimensionare interventi invasivi di consolidamento.
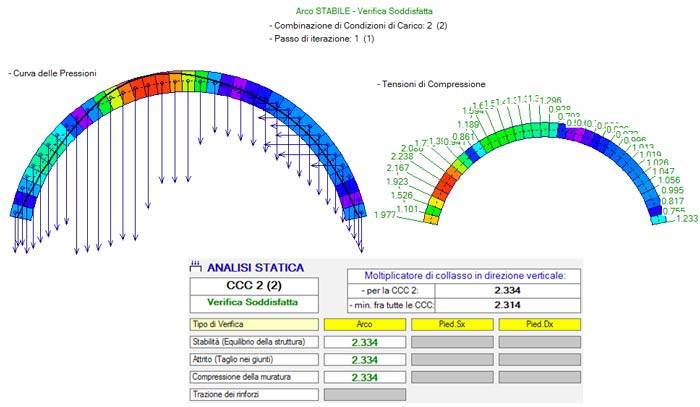
Figura 4
Per maggiori dettagli su questo esempio applicativo e approfondimenti sulle funzionalità di Aedes.SAV in relazione all'influenza della spinta passiva consultare i contenuti (documentazione e file per il software SAV) in download presenti sul sito di Aedes Software

Ingegneria Strutturale
Tutto quello che riguarda il tema dell’ingegneria strutturale: innovazione digitale, modellazione e progettazione, tecniche di costruzione e di...

Muratura
News e articoli che riguardano la soluzione della muratura nelle costruzioni, sia come elemento strutturale che come elemento di tamponamento:...

Software Strutturali
Tutto quello che riguarda il tema dei software di calcolo strutturale: modellazione, progettazione, innovazione, normativa, tips & tricks,...

