Influenza della variabilità delle proprietà meccaniche e geometriche sulla fragilità di ponti Maillart in c.a.

I ponti ad arco "Maillart" sono caratterizzati da un impalcato molto rigido e da una volta esile e larga

Negli ultimi anni, la valutazione delle condizioni di sicurezza rispetto ai carichi attuali dei ponti esistenti è diventata di prioritaria importanza per i gestori di ponti e infrastrutture. Infatti, il livello di sicurezza di un ponte esistente è spesso inadeguato a causa di diversi fattori: il numero sempre crescente di veicoli e, quindi, l’incremento dei carichi in esercizio indotti dal traffico, il degrado dei materiali (corrosione delle armature, carbonatazione del calcestruzzo) accentuato dall’assenza o l’inefficacia di programmi di manutenzione e dalle condizioni ambientali, la necessità di tener conto di azioni sismiche spesso non considerate o sottostimate all’epoca del progetto.

Condizioni ambientali e di carico modificate possono causare variazioni della resistenza strutturale, pregiudicando la sicurezza dei ponti sia in condizioni ultime che di esercizio. Ciò comporta che molti ponti esistenti potrebbero non soddisfare gli attuali standard di normativa.

I recenti crolli di ponti verificatisi in Italia, primo tra tutti il Viadotto "Polcevera" di Genova nel 2018, ma anche strutture minori come il ponte di Albiano Magra (2020), hanno contribuito ad evidenziare i principali problemi strutturali ed i rischi che possono interessare il patrimonio infrastrutturale italiano. Sia i collassi disastrosi che il danneggiamento diffuso hanno, infatti, dimostrato che, anche per i soli carichi gravitazionali attualmente agenti, le prestazioni strutturali dei ponti esistenti potrebbero essere insufficienti. Queste considerazioni hanno dato lo spunto per avviare negli ultimi anni diffuse campagne di va- lutazione del rischio strutturale per ponti e infrastrutture, che, in caso di danno, potrebbero comportare significative perdite economiche e sociali.

Un ulteriore problema, molto sentito in Italia, è dato dall’assenza di un dettagliato catalogo delle infrastrutture esistenti che rende ancora più difficile il ruolo degli enti gestori. Un esempio della particolarità dello scenario infrastrutturale italiano è rappresentato dal seguente dato (De Matteis et al., 2019): nel Febbraio 2019, non era noto l’ente proprietario per circa 1000 strutture tra ponti e viadotti.

Sebbene nel patrimonio infrastrutturale italiano dei ponti in calcestruzzo armato quelli a ‘travata’ siano i più ricorrenti, una discreta percentuale è rappresentata dai ponti ‘ad arco’. Tali ponti, progettati e costruiti soprattutto negli anni ‘50 del secolo scorso e, nella maggior parte dei casi, sottodimensionati per le condizioni di servizio odierne, richiedono particolare attenzione a causa delle loro specifiche peculiarità (arco progettato come funicolare dei pesi propri, pilastri tozzi alla chiave dell’arco, interazione impalcato-arco) che rendono particolarmente complessa la valutazione del loro comportamento sotto azioni sia statiche che dinamiche.

Nell’ambito dei ponti ad arco in c.a., il presente lavoro focalizza l’attenzione sui cosiddetti ponti ‘Maillart’, caratterizzati da un impalcato molto rigido e da una volta esile e larga, collegati tra loro da colonne o pareti molto snelle. Queste strutture prendono il nome dall’ingegnere svizzero Robert Maillart che per primo pensò di invertire il classico rapporto di inerzia tra impalcato e arco e riuscì ad ottenere una netta riduzione del momento e del taglio agenti nell’arco.

Tali ponti si inquadrano nelle cosiddette strutture ad “impalcato collaborante”, in cui quest’ultimo, chiamato ad esplicare una funzione statica, non costituisce più un semplice mezzo di trasmissione dei carichi, ma contribuisce alla capacità portante dell’intera struttura. Nei ponti ‘Maillart’, la volta ha il compito di sopportare i carichi gravitazionali da peso proprio attraverso un regime principalmente di compressione, ottenuto progettando la forma dell’arco in maniera da essere funicolare dei pesi propri. L’impalcato, invece, costituito da travi di elevata rigidezza, è deputato ad assorbire le sollecitazioni flessionali derivanti dai carichi accidentali. In Figura 1 si riportano due esempi di ponti ad arco tipo “Maillart” costruiti in Italia a partire dal 1960: il ponte “Ciolo” (Fig. 1a) e il viadotto “Canalone” (Fig. 1b).

Per questa tipologia di ponti ad arco informazioni su dimensioni e tipologia degli elementi, dettagli costruttivi sulle armature e sulle proprietà dei materiali sono disponibili per un numero ridotto di casi. Gli intervalli tipici di variabilità delle geometrie e delle proprietà meccaniche sono stati valutati basandosi su dati disponibili per circa 90 ponti ad arco esistenti (Crisci et al., 2021). Sulla base di questi intervalli, è stato generato un campione di ponti ad arco (1500) simulati con caratteristiche geometriche e meccaniche compatibili con le variabilità osservate (Crisci et al., 2021).

Sugli elementi di tale campione sono state sviluppate numerose analisi strutturali lineari e non lineari finalizzate ad investigare la vulnerabilità sismica dei ponti Maillart con diversi approcci: 1) analisi dinamiche non lineari condotte su una singola struttura del campione al variare dell’input sismico (Crisci et al., 2020b, Crisci et al., 2022); 2) analisi dinamiche lineari su tutto il campione (quindi su larga scala) al fine di valutare l’effetto della variabilità dei principali parametri geometrici nell’ambito del campione stesso (Crisci et al., 2020a).

Questo lavoro si propone l’obiettivo di estendere le analisi non lineari già condotte sulla singola struttura al variare dell’input sismico anche alla larga scala portando in conto la variabilità sia dei parametri geometrici sia delle proprietà dei materiali considerati nella generazione del campione, ma senza, tuttavia, dover svolgere le analisi non lineari su tutti gli elementi del campione. Per ridurre il numero di ana- lisi non-lineari da svolgere sono state utilizzate procedure di campionamento statistico note in letteratura (Vamvatsikos, 2014).

Successivamente, i risultati delle analisi non lineari sono stati sintetizzati in ter- mini di vulnerabilità nei riguardi dell’azione sismica attraverso opportune funzioni di fragilità costruite basandosi sulla metodologia Cloud (Jalayer et al., 2012) già applicata in (Crisci et al., 2020b, Crisci et al., 2022). Le analisi dinamiche non lineari sono sta- te realizzate generando dettagliati modelli tridimensionali dei ponti esaminati nel software OpenSees.
I risultati di questo studio, in un eventuale scenario post-terremoto, consentirebbero di stimare rapidamente i potenziali danneggiamenti su ponti ad arco in c.a. e di indirizzare le operazioni e gli interventi strutturali post-evento sismico.

Definizione del campione per analisi a larga scala

Procedura di campionamento

In generale, dato un qualsiasi modello strutturale, i due principali fattori che contribuiscono all'incertezza nella sua risposta sismica sono: (i) la variabilità dell’input sismico, e (ii) la variabilità dei parametri strutturali del modello, ovvero i parametri geometrici e/o meccanici. La prima può essere portata in conto analizzando la risposta dello stesso modello strutturale sotto molteplici accelerogrammi, come ad esempio viene fatto attraverso l’analisi dinamica incrementale, IDA (Vamvatsikos e Cornell 2002), o attraverso la Cloud Analysis (Jalayer, 2012).

La variabilità dei parametri strutturali del modello viene, invece, definita variabilità “epistemi- ca” e può essere aggiunta alla precedente in analisi dinamiche non lineari.

Tuttavia, l’applicazione su larga scala di analisi dinamiche non lineari combinate con approcci di simulazione Monte Carlo o con altri metodi di campionamento, come il Latin Hypercube Sampling (LHS), finalizzati a portare in conto la variabilità epistemica, potrebbe essere for- temente limitata dall’enorme aumento del numero di analisi. Se si volessero considerare tutti i parametri di incertezza, determinare l’influenza di più parametri casuali potrebbe diventare proibitivo in termini di tempo. Il metodo LHS (Novák et al., 2014) appartiene alla categoria delle tecniche di campionamento avanzate in grado di fornire un’ottima stima della risposta statistica di una popolazione anche simulandone piccoli campioni.

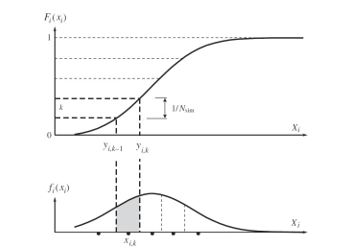
Più precisamente, il metodo LHS è considerato una tecnica di riduzione della varianza, poiché fornisce una varianza minore rispetto al campionamento con la tecnica Monte Carlo, a parità di dimensione del campione. La caratteristica fondamentale del metodo LHS è che ogni distribuzione cumulata, relativa ai parametri di definizione del campione da simulare, viene suddivisa in Nsim intervalli (con Nsim numero di simulazioni), tutti uguali, i cui valori medi sono utilizzati nel processo di simulazione. I valori medi vengono selezionati come punti centrali dei vari intervalli direttamente sulla funzione di densità di probabilità. La figura 2 riporta graficamente la selezione degli intervalli e l’individuazione dei punti centrali.

Per ridurre gli oneri computazionali ed ottenere risultati che portino in conto la variabilità epistemica oltre all’input sismico, l’approccio generale proposto da (Vamvatsikos, 2014) può essere applicabile per analisi di vulnerabilità su larga scala. Dato ad esempio un campione di 100 strutture con caratteristiche geometriche o meccaniche diverse ed un set di 100 accelerogrammi, tipicamente si dovrebbero eseguire un totale di 100x100 (10000) analisi, se il comportamento di ogni struttura venisse studiato per gli stessi 100 accelerogrammi selezionati. Secondo (Vamvatsikos, 2014), in maniera alternativa, l’insieme delle 10000 analisi può essere partizionato in 100 potenziali estrazioni, ciascuna delle quali corrisponde ad una sola delle 100 analisi che andrebbero eseguite per ogni struttura.

In questo modo, il numero di analisi da eseguire si ridurrebbe ad un numero (100), esattamente pari al numero di accelerogrammi selezionati. Questo approccio viene indicato in letteratura come assegnazione 1 a 1 (1 struttura per 1 accelerogramma) e permette un vantaggio sempre maggiore in termini di oneri computazionali al crescere del numero di variabili considerate.

L'ARTICOLO CONTINUA NEL PDF IN ALLEGATO...

La presente memoria è tratta da Italian Concrete Conference - Napoli, 12-15 ottobre 2022
Evento organizzato da aicap e CTE