Un metodo statico non lineare per la progettazione sismica di ponti con spalla integrale ai sensi del nuovo Eurocodice 8

Negli ultimi decenni un nuovo tipo di ponte privo di giunti è stato introdotto in Europa, ovvero quello con la spalla integrale. Nei ponti integrali gli spostamenti dell’impalcato dipendono dagli spostamenti delle sottostrutture e dalla flessibilità del sistema terreno-fondazione, dunque, il comportamento di tali opere è fortemente influenzato dall’interazione terreno-struttura la quale complica l’analisi. Ad oggi non ci sono metodi di analisi codificati per questo tipo di opere, specialmente rispetto ad azioni sismiche.

Per questo motivo un modello dinamico non-lineare proposto precedentemente è stato esteso e usato per calibrare un modello statico equivalente per la progettazione, basato sulla descrizione dell’interazione terreno-struttura attraverso travi di Winkler su un sottofondo di molle non-lineari, mentre impedenze statiche sono usate per le fondazioni su pali. Su tali modelli è stato svolto uno studio parametrico per valutarne la robustezza.

Nei ponti integrali il problema principale è che la struttura è influenzata dall’interazione terreno-struttura

Negli ultimi 60 anni, per ponti con luci medio piccole, è stata sviluppata una nuova tipologia con spalla integrale. Un ponte integrale è caratterizzato dall’avere una connessione monolitica tra impalcato e spalle eliminando, quindi, giunti di espansione e apparecchi d’appoggio permettendo una riduzione dei costi di costruzione e manutenzione (Dicleli & Erhan 2013, Lafave et al. 2016, Dicleli 2016, Caristo et al. 2018).

Per questa ragione, prima negli Stati Uniti e successivamente in Europa, questo tipo di schema strutturale è diventato sempre più popolare (Burke 2009, White et al. 2010). Da un punto di vista della progettazione il problema principale dei ponti integrali è che il comportamento globale della struttura è fortemente influenzato dall’interazione terreno-struttura. Infatti, già per deformazioni termiche stagionali, l’impalcato causa spostamenti nelle sottostrutture e questo porta a fenomeni d’interazione terreno-struttura (David & Forth 2011, Erhan & Dicleli 2014, Cole & Rollins 2006, Faraji et al. 2001).

Questi problemi sono ancora più amplificati nel caso di analisi dinamica e, in particolare, nel caso di azioni sismiche. Per questa ragione, ad oggi, non c’è una metodologia di analisi accettata e codi- ficata per la progettazione sismica di ponti integrali. Infatti, le normative in vigore nei vari stati per la progettazione di questo tipo di opere sono spesso limitate alle azioni statiche basandosi su evidenze sperimentali (Dicleli & Albhaisi 2003, Zordan et al. 2011, Dhar & Dasgupta 2019). Di seguito, quindi, si propone un metodo di analisi per la progettazione sismica di ponti integrali basandosi sulla descrizione dell’interazione terreno-struttura tramite travi di Winkler su molle non-lineari.

Breve descrizione del modello dinamico non-lineare

In questa sezione viene brevemente esposto il modello dinamico non-lineare dal quale quello statico semplificato è derivato. Il modello usa travi su un sottofondo di Winkler non-lineare per tenere conto dell’interazione terreno-struttura. Inoltre, il comportamento a taglio del deposito di terreno è modellato esplicitamente usando sempre elementi non-lineari.
Questo modello, inizialmente proposto da Franchin e Pinto nel 2014, è stato esteso in Marchi (2022) e calibrato contro un modello agli elementi finiti di ordine superiore in Marchi et al. 2022.
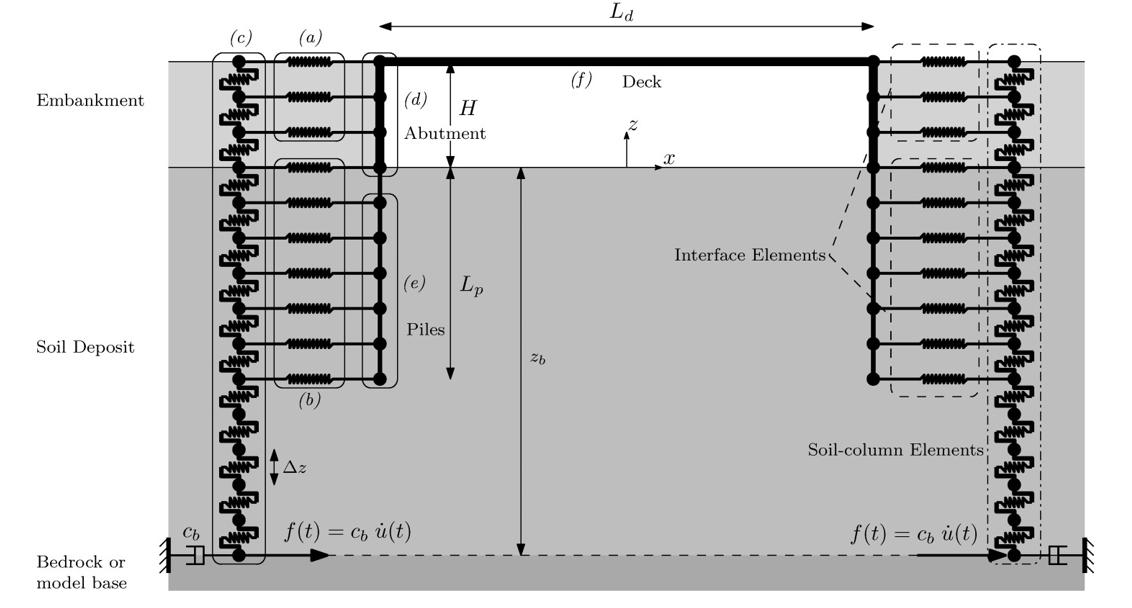
Il modello presenta, in particolare, elementi che descrivono il comportamento dinamico a taglio del deposito di terreno ed elementi di interfaccia che descrivono il terreno mobilitato durante il sisma dagli spostamenti della struttura rispetto al deposito (Figura 1).

Gli elementi strutturali sono modellati usando elementi elastici lineari dato che questo è un modello utilizzato per la progettazione e, per questo tipo di strutture, è richiesto che gli elementi rimangano sostanzialmente entro il limite di snervamento (Figura 1 (d) e (e)).

Questo modello descrive, in particolare, il comportamento longitudinale (lungo l’asse x) di ponti integrali senza angolo di sghembo. Inoltre, la spalla è sostenuta da una singola fila di pali e non presenta platea di fondazione.

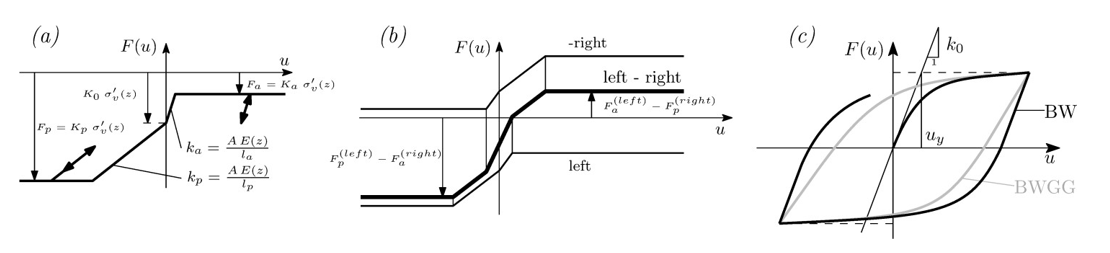
Gli elementi che descrivono il comportamento a taglio del deposito presentano solamente il grado di libertà lungo l’asse x (Figura 1 (c)). Il modello costitutivo di Bouc-Wen, nella versione modificata da Gerolymos e Gazetas (2005), è usato per approssimare il comportamento a taglio del terreno (Figura 2c). Il legame costitutivo considerato è definito dalla seguente equazione (si noti che il rapporto di incrudimento α è posto pari a zero):

F(u) = k0 u_y ζ(t)

dove la funzione interna ζ(t), che descrive il comportamento isteretico, è definita tramite la seguente equazione differenziale ordinaria:

ζ(t)/δt = θ ů(t)/uy {1+|ζ(t)|ⁿ[γ+β sgn(ů(t) ζ(t))]}

dove l’usuale parametro di Bouc-Wen A = γ + β è posto pari a uno. La funzione θ approssima il comportamento degradante del terreno durante la plasticizzazione ed è definita come:

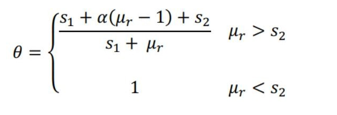
dove s₁ è un parametro adimensionale che controlla il degrado della rigidezza e s2 è un valore caratteri- stico di duttilità in deformazione oltre il quale l’effetto del degrado della rigidezza è attivato (Gerolymos & Gazetas 2005). I parametri di questo modello costitutivo (n, γ, β, s₁, s₂ e γ_y) sono presi da Drosos et al. (2012) in funzione del tipo di terreno (attraverso l’indice di plasticità) e della pressione di confinamento.

I parametri meccanici introdotti nella figura 2 sono u_y = γ_y Δ_z e k₀ = G0(z) A_s / Δ_z, dove A_s è l’area degli elementi di deposito, G0 il modulo di taglio a piccole deformazioni e Δz l’altezza dell’elemento. L’area degli elementi di deposito è assunta sufficientemente grande da assicurare che il comportamento degli elementi non sia influenzato dalla risposta della struttura. Ciò è ottenuto aumentando di 10 volte la lunghezza di rilevato collaborante Le = 5 H dalla quale l’area, e quindi anche la massa, di terreno è calcolata.

L’azione sismica è applicata alla base della colonna di terreno tramite una forza proporzionale alla velocità del segnale ed al coefficiente dello smorzatore che descrive il comportamento assorbente della base del modello verso onde di taglio incidenti (Ly- smer & Kuhlemeyer 1969). La forza applicata alla base è, quindi, pari a:

f(t) = c_b ů(t,z_b) = [ρ_b V_s,b A_s(z_b)] u(t,z_b)/δt

dove ρ_b e V_s,b sono rispettivamente la densità e la velocità delle onde di taglio alla base del modello, mentre As(zb) è l’area della colonna di terreno alla sua base (Kramer 1996). La funzione ů(t,z_b) rappresenta lo spostamento orizzontale all’affioramento ri- gido di terreno come descritto in Joyner & Chen (1975).
Gli elementi di interfaccia sono i più importanti nella definizione del modello, poiché sono quelli che definiscono l’interazione terreno-struttura (Figura 1 (a) e (b)).

Nel modello proposto questi presentano un legame costitutivo in sola compressione lineare a tratti con differenti soglie per tenere in conto della condizione limite attiva e passiva. Il modello considera, inoltre, anche differenti rigidezze tra la zona attiva e quella passiva (Figura 2a e 2b). Le condizioni limite del terreno (attive e passive) sono descritte tramite coefficienti di spinta (K_a e K_p rispettivamente) descritti in Lancellotta (2002). Le rigidezze nel lato attivo e passivo dipendono dalle lunghezze attive e passive l_a e l_p definite nel lavoro di Becci & Nova (1987), il quale rappresenta la base dell’analisi semplificata tramite travi di Winkler per muri di contenimento del terreno flessibili (Franchin et al. 2007).

... Continua la lettura nel PDF.